（本小题满分12分）盒子内有大小相同的9个球,其中2个红色小球,3个白色小
球,4个黑色小球,规定取出1红色小球得到1分, 取出1白色小球得到0分, 取出1个黑色小球得到-1分,现从盒子中任取3个小球。
(Ⅰ)求取出的3个球颜色互不相同的概率;
(Ⅱ)求取出的3个球得分之和恰好为1分的概率;
(Ⅲ)设ξ为取出的3个球中白色球的个数,求ξ的分布列及数学期望.
（本小题满分12分）．在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，
现从甲、乙两个盒子中各取出1个球，每个小球被取出的可能性相等
（I）求取出的两个球上标号为相邻整数的概率；
（II）求取出的两个球上标号之和能被3整除的概率.
（本小题满分12分）．已知
，
函数
的最小正周期为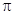
( 其中
为正常数，
)
（I）求的值和函数
的递增区间；
（II）在△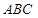
中，若
，且
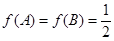，求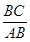
．(本小题满分l0分)选修4—5：不等式选讲
已知函数
．(I)求不等式
≤6的解集；(Ⅱ)若关于
的不等式>
恒成立，求实数的取值范围。
(本小题满分10分)选修4—4：坐标系与参数方程
在平面直角坐标系
中，以原点
为极点，
轴为极轴建立极坐标系，曲线C1的方程
为
（
为参数），曲线C2的极坐标方程为：
，若曲线C1与
C2相交于A、B两点． (I)求|AB|的值；(Ⅱ)求点M(-1，2)到A、B两点的距离之积．
(本小题满分10分)选修4—1：几何证明选讲
如图，AB为圆
的直径，P为圆外一点，过P点作PC
AB于C，交圆于D点，PA
交圆于E点，BE交PC于F点．(I)求证：
；(Ⅱ)求证：
