(本小题满分10分)选修4—4:坐标系与参数方程
在平面直角坐标系 中,以原点
中,以原点 为极点,
为极点, 轴为极轴建立极坐标系,曲线C1的方程
轴为极轴建立极坐标系,曲线C1的方程
为 (
( 为参数),曲线C2的极坐标方程为:
为参数),曲线C2的极坐标方程为: ,若曲线C1与
,若曲线C1与
C2相交于A、B两点. (I)求|AB|的值;(Ⅱ)求点M(-1,2)到A、B两点的距离之积.
已知函数f(x)=cosx•sin(x+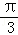 )﹣
)﹣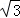 cos2x+
cos2x+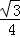 ,x∈R.
,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在闭区间[﹣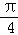 ,
,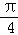 ]上的最大值和最小值.
]上的最大值和最小值.
数列{an}通项公式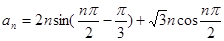 ,前n项和为Sn,则S2015=
,前n项和为Sn,则S2015=
设函数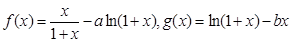
(1)若函数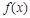 在
在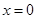 处有极值,求函数
处有极值,求函数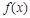 的最大值;
的最大值;
(2)是否存在实数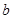 ,使得关于
,使得关于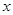 的不等式
的不等式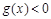 在
在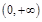 上恒成立?若存在,求出
上恒成立?若存在,求出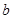 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)证明:不等式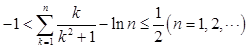
设函数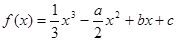 ,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
(1)求b,c的值;
(2)若a>0,求函数f(x)的单调区间;
(3)设函数g(x)=f(x)+2x,且g(x)在区间(-2,-1)内存在单调递减区间,求实数a的取值范围.
数列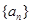 的前
的前 项和是
项和是 ,且
,且 .
.
(1)求数列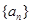 的通项公式;
的通项公式;
(2)记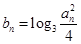 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: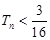 .
.