设函数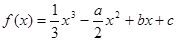 ,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
(1)求b,c的值;
(2)若a>0,求函数f(x)的单调区间;
(3)设函数g(x)=f(x)+2x,且g(x)在区间(-2,-1)内存在单调递减区间,求实数a的取值范围.
数列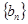 是递增的等比数列,且
是递增的等比数列,且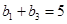 ,
,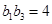 .
.
求数列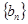 的通项公式;
的通项公式;
若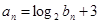 ,求证数列
,求证数列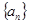 是等差数列;
是等差数列;
若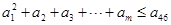 ,求
,求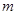 的最大值.
的最大值.
如图,已知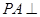 面
面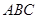 ,
,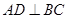 于D,
于D,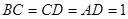 。
。
(1)令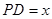 ,
,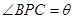 ,试把
,试把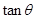 表示为
表示为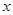 的函数,并求其最大值;
的函数,并求其最大值;
(2)在直线PA上是否存在一点Q,使得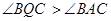 ?
?
若实数 、
、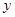 、
、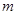 满足
满足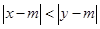 ,则称
,则称 比
比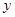 接近
接近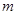 .
.
(1)若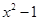 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)已知函数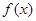 的定义域
的定义域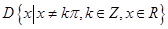 .任取
.任取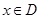 ,
,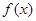 等于
等于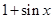 和
和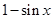 中接近0的那个值.写出函数
中接近0的那个值.写出函数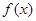 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
已知复数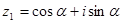 ,
, 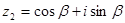 ,
, 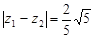 ,
,
求:(1)求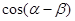 的值;(2)若
的值;(2)若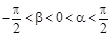 ,且
,且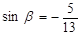 ,求
,求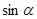 的值.
的值.
(本小题14分)已知函数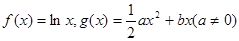
(Ⅰ)若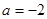 时,函数
时,函数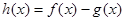 在其定义域上是增函数,求b的取值范围;
在其定义域上是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设函数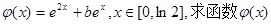 的最小值;
的最小值;
(Ⅲ)设函数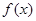 的图象C1与函数
的图象C1与函数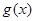 的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.