如图所示为研究电子枪中电子在电场中运动的简化模型示意图．在Oxy平面的ABCD区域内，存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ，两电场的边界均是边长为L的正方形(不计电子所受重力)．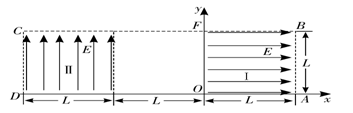
在该区域AB边的中点处由静止释放电子，求电子离开ABCD区域的位置．
在电场Ⅰ区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置．
若将左侧电场Ⅱ整体水平向右移动L/n(n≥1)，仍使电子从ABCD区域左下角D处离开(D不随电场移动)，求在电场Ⅰ区域内由静止释放电子的所有位置．
随着机动车数量的增加，交通安全问题日益凸显。分析交通违法事例，将警示我们遵守交通法规，珍惜生命。一货车严重超载后的总质量为49t，以54km/h的速率匀速行驶。发现红灯时司机刹车，货车即做匀减速直线运动，加速度的大小为2.5m/s2（不超载时则为5m/s2）。若前方无阻挡，问从刹车到停下来此货车在超载及不超载时分别前进多远？
若超载货车刹车时正前方25m处停着总质量为1t的轿车，两车将发生碰撞，设相互作用0.1 s后获得相同速度，问货车对轿车的平均冲力多
在如图所示的装置中，两个光滑的定滑轮的半径很小，表面粗糙的斜面固定在地面上，斜面的倾角为θ＝30°。用一根跨过定滑轮的细绳连接甲、乙两物体，把甲物体放在斜面上且连线与斜面平行，把乙物体悬在空中，并使悬线拉直且偏离竖直方向α＝60°。现同时释放甲乙两物体，乙物体将在竖直平面内振动，当乙物体运动经过最高点和最低点时，甲物体在斜面上均恰好未滑动。已知乙物体的质量为m＝1㎏，若取重力加速度g＝10m/s2。求：甲物体的质量及斜面对甲物体的最大静摩擦力。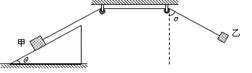
在一个倾斜的长冰道上方,一群孩子排成队,每隔1 s有一个
小孩子下滑,一游客对着冰道上的孩子拍下一张照片,如图9所示照片上
有甲、乙、丙、丁四个孩子.他根据照片与实物的比例推算出乙与甲
和乙与丙两孩子间的距离分别为12.5 m和17.5 m,请你据此求解下列问题.
(g取10 m/s2)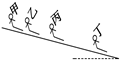
若不考虑一切阻力,小孩下滑加速度是多少?
拍照时,最下面的小孩丁的速度是多大?
拍照时,在小孩甲上面的冰道上下滑的小孩子不会超过几个?
1934年约里奥—居里夫妇用α粒子轰击静止的Al，发现了放射性磷P和另一种粒子，并因这一伟大发现而获得诺贝尔物理学奖．写出这个过程的核反应方程式．
若该种粒子以初速度v0与一个静止的12C核发生碰撞，但没有发生核反应，该粒子碰后的速度大小为v1，运动方向与原运动方向相反，求碰撞后12C核的速度．
如图所示，一电荷量q=3×10-5C带正电的小球，用绝缘细线悬于竖直放置足够大的平行金属板中的O点。电键S合上后，当小球静止时，细线与竖直方向的夹角α=37°。已知两板相距d=0.1m，电源电动势
=15V，内阻r=0.5Ω，电阻R1=3Ω，R2=R3= R4 =8Ω。g取10m/s2，已知
，
。求：
电源的输出功率；
两板间的电场强度的大小；
带电小球的质量。