1934年约里奥—居里夫妇用α粒子轰击静止的Al,发现了放射性磷P和另一种粒子,并因这一伟大发现而获得诺贝尔物理学奖.写出这个过程的核反应方程式.
若该种粒子以初速度v0与一个静止的12C核发生碰撞,但没有发生核反应,该粒子碰后的速度大小为v1,运动方向与原运动方向相反,求碰撞后12C核的速度.
如图,一水平放置的平行板电容量的两极板间距为d=15cm,极板间有恒定电压,上极板中心有一小孔(小孔对电场的影响可忽略不计).在小孔正上方距上板h=10cm处的P点,一质量为m=3×10﹣6kg,带电量q=﹣2.5×10﹣8C的油滴自P点自由下落,经过小孔进入电容器,到达N板处(未与极板接触)速度恰为零,问(g=10m/s2):
(1)M、N两板哪个极板电势高?其间电场强度是多大?
(2)若将N板向上平移5cm,求从P点自由下落的相同油滴在电场中与M板的最大距离.
如图的装置放置在真空中,炽热的金属丝可以发射电子(初速为零),金属丝和竖直金属板之间加以电压U1,发射出的电子被加速后,从金属板上的小孔S射出.装置右侧有两个相同的平行金属极板水平正对放置,板长为l,相距为d,两极板间加以电压U2的偏转电场.从小孔S射出的电子恰能沿平行于板面的方向由极板左端中间位置射入偏转电场.已知电子的电荷量e,质量为m,忽略金属极板边缘对电场的影响,不计电子受到的重力.求:
(1)电子射入偏转电场时的速度;
(2)电子射出偏转电场时在竖直方向上的侧移量y.
在如图所示的电路中,R1=2Ω,R2=4Ω,当开关S闭合时,R2上消耗的电功率为4W,当开关S断开时,电压表示数为4.5V,求电源的电动势和内阻值.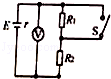
如图,将电荷量为q=+3.0×10﹣6C的试探电荷从匀强电场中的A点沿电场线移动到B点,已知AB=6cm,电场力做的功为W=3.6×10﹣6J,求:
(1)A,B两点的电势差.
(2)匀强电场的电场强度E.
在地面上方,一小圆环A套在一条均匀直杆B上,A和B的质量均为m,若它们之间发生相对滑动时,会产生f=0.5mg的摩擦力.开始时A处于B的最下端,B竖直放置,在A的下方h=0.2m处,存在一个“相互作用”区域C,区域C的高度d=0.30m,固定在空中如图中划有虚线的部分,当A进入区域C时,A就受到方向向上的恒力F作用。F=2mg,区域C对杆B不产生作用力.A和B一起由静止开始下落,已知杆B落地时A和B的速度相同.不计空气阻力,重力加速度g=10m/s2.求: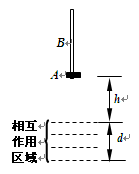
(1)A在相互作用区域内,A、B的加速度?
(2)A刚离开作用区域时,A、B的速度?
(3)杆B的长度L至少应为多少?