如图所示，在xOy平面的第一象限内存在着方向垂直纸面向外，磁感应强度为B的匀强磁场，在第四象限内存在方向沿负x方向的匀强电场。从y轴上坐标为（0，a）的P点同时沿垂直磁场方向向磁场区发射速度大小不是都相等的带正电的同种粒子，粒子的速度方向在与y轴正方向成30°～150°角的范围内，结果所有粒子经过磁场偏转后都垂直打到x轴上，然后进入第四象限内的电场区。已知带电粒子电量为+q，质量为m，不计粒子重力和粒子间的相互作用力。
求全部粒子经过x轴的时间差。
求粒子通过x轴时的位置范围。
已知从P点发出时速度最大的粒子受到的磁场力与它在电场中
受到的电场
力大小相等，求从P点发出时速度最小的粒子穿过电场后在y轴上的Q点射出电场时的速度大小v。
如图所示，一内壁光滑的细管弯成半径为R=0.4m的半圆形轨道CD,竖直放置，其内径略大于小球的直径，水平轨道与竖直半圆轨道在C点连接完好。置于水平轨道上的弹簧左端与竖直墙壁相连，B处为弹簧的自然状态。将一个质量为m=0.8kg的小球放在弹簧的右侧后，用力向左侧推小球而压缩弹簧至A处，然后将小球由静止释放，小球运动到C处后对轨道的压力为F1=58N。水平轨道以B处为界，左侧AB段长为x=0.3m，与小球的动摩擦因数为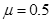
，右侧BC段光滑。g=10m/s2，求：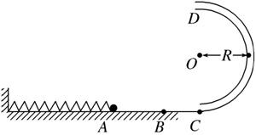
（1）弹簧在压缩时所储存的弹性势能。
（2）小球运动到轨道最高处D点时对轨道的压力大小。
某研究小组为测量一个遥控电动小车的额定功率，进行了如下实验：
①用天平测出电动小车的质量为0.4kg；
②将电动小车、纸带和打点计时器按如图所示安装；
③接通打点计时器（其打点周期为0.02s）；
④使电动小车以额定功率加速运动，达到最大速度一段时间后关闭小车电源，待小车静止时再关闭打点计时器（设小车在整个过程中小车与纸带所受的阻力恒定）。在上述过程中，打点计时器在纸带上所打的部分点迹如图所示（已知纸带左端与小车相连）请分析纸带数据，回答下列问题：
（1）电动小车运动的最大速度为_______ m／s
（2）电动小车关闭电源后加速度大小为m/s2
（3）电动小车的额定功率为W。
一辆值勤的警车停在平直公路边，当警员发现从他旁边以v="10" m／s的速度匀速行驶的货车有违章行为时，决定前去追赶，经t0="2s" 警车发动起来，以加速度a="2" m/s2做匀加速运动，试问：
（1）在警车追上货车之前，两车间的最大距离是多少?
（2）若警车能达到的最大速度是vm="12" m/s，达到最大速度后匀速运动。则警车发动起来后至少要多长的时间才能追上违章的货车?
在某路段相邻较近的两红绿灯路口之间，一辆汽车在第一个路口从静止开始以5m/s2的加速度做匀加速运动，行驶40m，立即以1.25 m/s2的加速度做匀减速直线运动，到达下一个路口时刚好停止，求：
（1）汽车从启动到停止所用的时间；
（2）两红绿灯路口间的距离．
一个小球从距离地面20m的高空自由下落，g取10m/s2，求
（1）小球落地时的速度大小？
（2）小球从开始运动到落地的总时间为多少？
（3）小球落地前最后1s内的位移大小？