质量为m、总电阻为R的导线做成边长为l的正方形线框MNPQ，并将其放在倾角为θ的平行绝缘导轨上，平行导轨的间距也为l，如图所示。线框与导轨之间是光滑的，在导轨的下端有一宽度为l（即ab=l）、磁感应强度为B的有界匀强磁场，磁场的边界aa′、bb′垂直于导轨，磁场的方向与线框平面垂直。某一次，把线框从静止状态释放，线框恰好能够匀速地穿过磁场区域。若当地的重力加速度为g，求：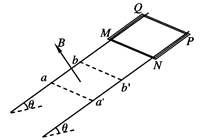
线框通过磁场时的运动速度；
开始释放时，MN与bb′之间的距离；
线框在通过磁场的过程中所生的热。
如图所示，半径R = 0.1m的竖直半圆形光滑轨道bc与水平面ab相切。质量m = 0.1kg的小滑块B放在半圆形轨道末端的b点，另一质量也为m= 0.1kg的小滑块A，以v0 = 2
m/s的水平初速度向B滑行，滑过s = 1m的距离，与B相碰，碰撞时间极短，碰后A、B粘在一起运动。已知木块A与水平面之间的动摩擦因数μ = 0.2。取重力加速度g = 10m/s²。A、B均可视为质点。求：
（1）A与B碰撞前瞬间的速度大小vA；
（2）碰后瞬间，A、B共同的速度大小v；
（3）在半圆形轨道的最高点c，轨道对A、B的作用力N的大小。
某同学是一位航天科技爱好者，当他从新闻中得知，中国航天科技集团公司将在2010年底为青少年发射第一颗科学实验卫星——“希望一号”卫星（代号XW-1）时，他立刻从网上搜索有关“希望一号”卫星的信息，其中一份资料中给出该卫星运行周期10.9min。他根据所学知识计算出绕地卫星的周期不可能小于83min，从而断定此数据有误。
已知地球的半径R=6.4×106m，地球表面的重力加速度g=10m/s2。请你通过计算说明为什么发射一颗周期小于83min的绕地球运行的人造地球卫星是不可能的。
如图所示，质量为2.0kg的木块放在水平桌面上的A点，受到一瞬时冲量后以某一速度在桌面上沿直线向右运动，运动到桌边B点后水平滑出落在水平地面C点。已知木块与桌面间的动摩擦因数为0.20，桌面距离水平地面的高度为1.25m，A、B两点的距离为4.0m， B、C两点间的水平距离为1.5m，g=10m/s2。不计空气阻力，求：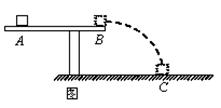
（1）滑动摩擦力对木块做功是多少；
（2）木块在A点时的动能；
（3）木块运动的总时间。
设雨点下落过程受到的空气阻力与雨点的横截面积S成正比，与雨点下落的速度v的平方成正比，即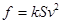
（其中k为比例系数）．雨点接近地面时近似看做匀速直线运动，重力加速度为g．若把雨点看做球形，其半径为r,球的体积为
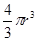，设雨点的密度为
，求：
(1)每个雨点最终的运动速度
（用、r、g、k表示）；
(2)雨点的速度达到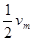
时，雨点的加速度a为多大？
在如图所示，x轴上方有一匀强磁场，磁感应强度的方向垂直于纸面向里，大小为B，x轴下方有一匀强电场，电场强度的大小为E，方向与y轴的夹角θ为45o且斜向上方。现有一质量为m电量为q的正离子，以速度v0由y轴上的A点沿y轴正方向射入磁场，该离子在磁场中运动一段时间后从x轴上的C点进入电场区域，该离子经C点时的速度方向与x轴夹角为45o。 不计离子的重力，设磁场区域和电场区域足够大。求：
|
（1）C点的坐标；
（2）离子从A点出发到第三次穿越x轴时的运动时间；