如图所示,两根平行光滑金属导轨位于水平面内,导轨间距L=20cm,电阻R=1.0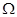 ;一金属杆垂直两轨静止在轨道上,轨道和金属杆的电阻不计,全部装置处于磁感应强度B=0.5T,方向竖直向下的匀强磁场中。现用一外力F沿轨道方向拉金属杆使之做匀加速运动,测得力F与时间t的关系如F-t图象所示,求金属杆的质量和加速度。
;一金属杆垂直两轨静止在轨道上,轨道和金属杆的电阻不计,全部装置处于磁感应强度B=0.5T,方向竖直向下的匀强磁场中。现用一外力F沿轨道方向拉金属杆使之做匀加速运动,测得力F与时间t的关系如F-t图象所示,求金属杆的质量和加速度。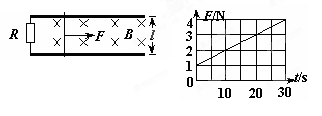
一质量为m=2×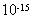 kg,电荷量q=-3×
kg,电荷量q=-3×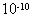 C的带电微粒,自A点垂直进入有一定宽度的匀强电场,从B点飞出时,速度
C的带电微粒,自A点垂直进入有一定宽度的匀强电场,从B点飞出时,速度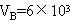 m/s,方向和电场线方向成120°角.已知A、B两点间沿电场线方向的距离为15cm,求
m/s,方向和电场线方向成120°角.已知A、B两点间沿电场线方向的距离为15cm,求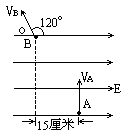
(1)B、A间的电势差
(2)微粒从A到B经历的时间
(3)匀强电场的宽度(微粒重力不计)
如图11所示,用一个平行于斜面向上的恒力将质量m=10.0kg的箱子从斜坡底端由静止推上斜坡,斜坡与水平面的夹角θ=37°,推力的大小F=100N,斜坡长度s=4.8m,木箱底面与斜坡的动摩擦因数μ=0.20。重力加速度g取10m/s2,且已知sin37°=0.60,cos=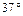 0.80。求:
0.80。求: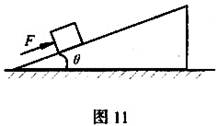
(1)木箱沿斜坡向上滑行的加速度的大小。
(2)木箱到滑斜坡顶端时速度的大小。
如图所示,坐标系xoy位于竖直平面内,所在空间有沿水平方向垂直于纸面向里的匀强磁场,磁感应强度大小为B,在x<0的空间内还有沿x轴负方向的匀强电场,场强大小为E。一个带正电的油滴经图中x轴上的M点,沿着直线MP做匀速运动,过P点后油滴进入x>0的区域,图中 。要使油滴在x>0的区域内做匀速圆周运动,需在该区域内加一个匀强电场。若带电油滴做匀速圆周运动时沿
。要使油滴在x>0的区域内做匀速圆周运动,需在该区域内加一个匀强电场。若带电油滴做匀速圆周运动时沿 弧垂直于x轴通过了轴上的N点,求:
弧垂直于x轴通过了轴上的N点,求:
(1)油滴运动速率的大小;
(2)在x>0的区域内所加电场的场强大小和方向;
(3)油滴从x轴上的M点经P点运动到N点所用的时间。
如图1 0所示电路中,电源内阻不计,三个小灯泡完全相同
0所示电路中,电源内阻不计,三个小灯泡完全相同
且外电路变化时每个灯泡两端的电压都不会超过其额定电
压,开始时只有S1闭合,当S 2也闭合后,下列说法正确的
2也闭合后,下列说法正确的
是 ( )
| A.灯泡L1变亮 |
| B.灯泡L2变亮 |
| C.电容器C的带电量将增加 |
| D.闭合S2的瞬间流过电流表的电流方向自右向左 |
为了安全,在公路上行驶的汽车之间应保持必要的距离,已知某高速公路的最高限速v="120" km/h。假设前方车辆因故障突然停止,后车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s。刹车时汽车受到阻力的大小f为汽车重力的0.40倍。该高速公路上汽车间的距离s至少应为多少?(取重力加速度g=10m/s2)