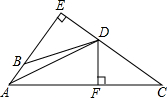
在长方形中画出5条线,把它分成的块数与画线的方式有直接关系.按如图1的方式画线,可以把它分成10块.(1)请你在图2中画出5条线,使得把这个长方形分成的块数最少(重合的线只看做一条),最少可分成 块;
(2)请你在图2中画出5条线,使得把这个长方形分成的块数最多,最多可分成 块.
(画出图形不写画法和理由)
(本小题满分6分)先化简,再求值: ,其中
,其中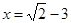 .
.
在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△A1B1C1,使点C1落在直线BC上(点Cl与点C不重合),
(1)当∠C=60°时,写出边AB1与边CB的位置关系(不要求证明);
(2)如图,当∠C>60°时,写出边AB1与边CB的位置关系,并加以证明;

(3)当∠C<60°时,请你在如图中用尺规作图法作出△AB1C1(保留作图痕迹,不写作法),再猜想你在(1)、(2)中得出的结论是否还成立并说明理由.
为了更好地治理小凌河水质,保护环境,市治污公司决定购买10台污水处理设备,现有A 、B两种设备,A 、B单价分别为a万元/台、 b万元/台,月处理污水分别为240吨/月、200吨/月,经调查,买一台A型设备比买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a、b的值.
(2)经预算,市治污公司购买污水处理器的资金不超过105万元,你认为该公司有哪几种购买方案?
(3)在(2)的条件下,若每月处理的污水不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的方案.
如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP垂直AD于P点,求证:BQ=2PQ.
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,
求证:AD是∠BAC的平分线.