如图10所示，已知A点的坐标为（-1，0），点B的坐标是（9,0）以AB为直径作⊙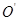
，交y轴负半轴于点C，连接AC、BC，过A、B、C作抛物线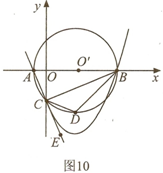
（1）求抛物线的解析式
（2）点E是AC延长线上的一点，∠BCE的平分线CD交⊙
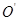于点D，连结BD求BD直线的解析式（3）在（2）的条件下，点P是直线BC下方的抛物线上一动点，当点P运动到什么位置时，△PCD的面积是△BCD面积的
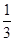，求此时点P的坐标
如图，河流的两岸PQ、MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD=50米，某人在河岸MN的A处测得∠DAN=35°，然后沿河岸走了120米到达B处，测得∠CBN=70°．求河流的宽度CE（结果保留两个有效数字）．
（参考数据：sin35°≈0．57，cos35°≈0．82，tan35°≈0．70，sin70°≈0．94，cos70°≈0．34，tan70°≈2．75）
如图，在□ABCD中，E ，F分别为边AB, CD的中点，连接DE, BF, BD．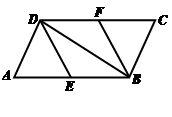
（1）求证：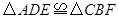
．
（2）当时，（添加一个条件），四边形BFDE是菱形？请证明你的结论．
如图，一次函数y1=2x+1的图像与反比例函数y2=
（k为常数，且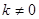
）的图像都经过点A（m,3）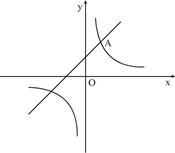
（1）求点A的坐标及反比例函数的表达式
（2）结合图像直接比较：当x＞0时，y1和y2的大小．
便民”水泥代销点销售某种水泥，每吨进价为250元，如果每吨销售价定为290元时，平均每天可售出16吨。
（1）若代销点采取降低促销的方式，试建立每吨的销售利润y（元）与每吨降低x（元）之间的函数关系式。
（2）若每吨售价每降低5元，则平均每天能多售出4吨，问：每吨水泥的实际售价定为多少元时，每天的销售利润平均可达720元。
如图，有一个可以自由转动的转盘被平均分成3个扇形，分别标有1、2、3三个数字，小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（若指针指在分界线时重转）．
（1）请你用树状图或列表的方法表示出每次游戏可能出现的所有结果；
（2）求每次游戏结束得到的一组数恰好是方程x2-3x+2=0的解的概率．