如图, 为直角三角形,
为直角三角形, ,
, ,
, ;四边形
;四边形 为矩形,
为矩形, ,
, ,且点
,且点 、
、 、
、 、
、 在同一条直线上,点
在同一条直线上,点 与点
与点 重合.
重合.
(1)求边
 的长;
的长;(2)将
 以每秒
以每秒 的速度沿矩形
的速度沿矩形 的边
的边 向右平移,当点
向右平移,当点 与点
与点 重合时停止移动,设
重合时停止移动,设 与矩形
与矩形 重叠部分的面积为
重叠部分的面积为 ,请求出重叠部分的面积
,请求出重叠部分的面积 (
( )与移动时间
)与移动时间 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);(3)在(2)的基础上,当
 移动至重叠部分的面积为
移动至重叠部分的面积为
 时,将
时,将 沿边
沿边 向上翻折,得到
向上翻折,得到 ,请求出
,请求出 与矩形
与矩形 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
用不等式表示下列关系.
(1) 与3的和的2倍不大于-5;
与3的和的2倍不大于-5;
(2)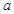 除以2的商加上4至多为6;
除以2的商加上4至多为6;
(3)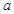 与
与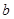 两数的平方和为非负数.
两数的平方和为非负数.
用不等式表示下列句子的含义.
(1)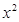 是非负数;
是非负数;
(2)老师的年龄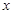 比赵刚的年龄
比赵刚的年龄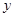 的
的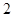 倍还大;
倍还大;
(3)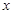 的相反数是正数;
的相反数是正数;
(4)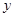 的
的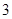 倍与
倍与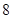 的差不小于
的差不小于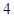 .
.
如图1,两个不全等的等腰直角三角形 和
和 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点 .
.
(1)在图1中,你发现线段 ,
, 的数量关系是,直线
的数量关系是,直线 ,
, 相交成度角.
相交成度角.
(2)将图1中的 绕点
绕点 顺时针旋转
顺时针旋转 角,这时(1)中的两个结论是否成立?请做出判断并说明理由.
角,这时(1)中的两个结论是否成立?请做出判断并说明理由.
(3)将图1中的 绕点
绕点 顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.
顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
如图,在⊙O中,∠ACB=∠BDC=60°,AC=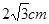 ,
,
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长