如图，在矩形ABCD中，AB=9，AD=12．动点E从点B出发，沿线段BC（不包括端点B、C）以每秒2个单位长度的速度，匀速向点C运动；动点F从点C出发，沿线段CD（不包括端点C、D）以每秒1个单位长度的速度，匀速向点D运动；点E、F同时出发，同时停止．连接AF并延长交BC的延长线于点M，再把AM沿AD翻折交CD延长线于点N，连接MN．设运动时间为t秒．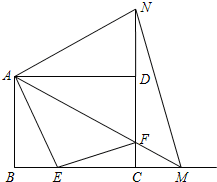
（1）当t为何值时，△ABE∽△ECF；
（2）在点E运动的过程中是否存在某个时刻使AE⊥AN？若存在请求出t的值，若不存在请说明理由；
（3）在运动的过程中，△AMN的面积是否变化？如果改变，求出变化的范围；如果不变，求出它的值．
用配方法解一元二次方程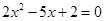
．请结合题意填空，完成本题的解答．
解：方程变形为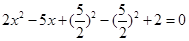
，.......................第一步
配方，得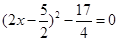
．.......................................第二步
移项，得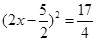
．..........................................第三步
两边开平方，得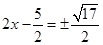
．...................................第四步
即
或
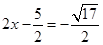．................................第五步
所以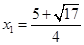
，
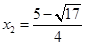．..................................第六步
（1）上述解法错在第 步；
（2）请你用配方法求出该方程的解．
解方程：
．
如图是1710的正方形网格，四边形ABCD的四个顶点都在网格的顶点上，我们把这样的四边形称作格点四边形．请在网格中画出一个与四边形ABCD相似但不全等的格点四边形EFGH．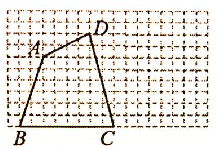
如图，抛物线y=﹣x2+bx+c交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．
（1）求抛物线的函数表达式；
（2）若点P在抛物线上，且S△AOP=4SBOC，求点P的坐标；
（3）如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．
已知：点D是等腰直角三角形ABC斜边BC所在直线上一点（不与点B重合），连接AD．
（1）如图1，当点D在线段BC上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．求证：BD=CE，BD⊥CE．
（2）如图2，当点D在线段BC延长线上时，探究AD、BD、CD三条线段之间的数量关系，写出结论并说明理由；
（3）若BD=
CD，直接写出∠BAD的度数．