如图,在△ABC中,AB=AC,点O为底边上的中点,以点O为圆心,1为半径的半圆与边AB相切于点D.
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当∠A=60°时,求图中阴影部分的面积.
解下列方程
(1) 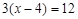 (2)
(2)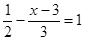
已知:如图1,一次函数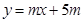 的图像与x轴、y轴分别交于点A、B,与函数
的图像与x轴、y轴分别交于点A、B,与函数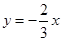 的图像交于点C,点C的横坐标为-3.
的图像交于点C,点C的横坐标为-3.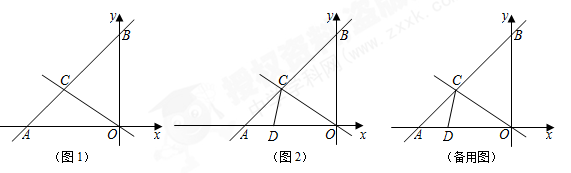
(1) 求点B的坐标;
(2) 若点Q为直线OC上一点,且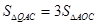 ,求点Q的坐标;
,求点Q的坐标;
(3) 如图2,点D为线段OA上一点,∠ACD=∠AOC.点P为x轴负半轴上一点,且点P到直线CD和直线CO的距离相等.
① 在图2中,只利用圆规作图找到点P的位置;
(保留作图痕迹,不得在图2中作无关元素.)
② 求点P的坐标.
已知:如图1,△ABC中,AB=13,BC=14,AC=15.将线段AB沿过点A的直线翻折,使得点B的对应点E恰好落在BC边上,折痕与BC边相交于点D,如图2所示.
(1) 求线段DE的长;
(2) 在图2中,若点P为线段AC上一点,且△AEP为等腰三角形,求AP的长.
小李在解决第(2)小题时的过程如下:
① 当EA=EP时,显然不存在;当AE=AP时,则AP=__________;(需填空)
② 对于“当PA=PE时的情形”,小李在解决时遇到了困难.小明老师对小李说:对于这个“直线形”图形直接解决困难时,我们可以建立平面直角坐标系,用一次函数的知识解决.如以点D为坐标原点,BC所在直线为x轴,然后求出AE中垂线的直线解析式,然后求出点P的坐标,最后用勾股定理求出AP的长……
请根据小明老师的提示完成第(2)题中②的求解,你也可以用自己的方法求出AP的长.
现有一个长、宽、高分别为5 dm、4 dm、3 dm的无盖长方体木箱(如图,AB=5 dm,BC=4 dm,AE=3 dm).
(1) 求线段BG的长;(2) 现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.
(请计算说明,木板的厚度忽略不计)
(本小题满分8分) 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示, 为方案一的函数图像,
为方案一的函数图像,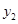 为方案二的函数图像.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
为方案二的函数图像.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):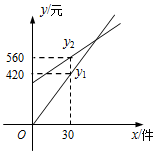
(1) 求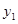 的函数解析式;
的函数解析式;
(2) 请问方案二中每月付给销售人员的底薪是多少元?
(3) 小丽应选择哪种销售方案,才能使月工资更多?