(本小题满分8分) 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,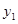 为方案一的函数图像,
为方案一的函数图像,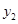 为方案二的函数图像.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
为方案二的函数图像.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题
(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):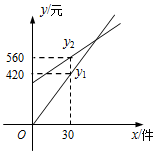
(1) 求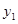 的函数解析式;
的函数解析式;
(2) 请问方案二中每月付给销售人员的底薪是多少元?
(3) 小丽应选择哪种销售方案,才能使月工资更多?
.
综合与实践
【问题情境】
数学活动课上,老师出示了一个问题:如图1,在正方形 中,E是BC的中点, , 与正方形的外角 的平分线交于 点.试猜想 与 的数量关系,并加以证明;
【思考尝试】
(1)同学们发现,取 的中点 ,连接 可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
【实践探究】
(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 ,可以求出 的大小,请你思考并解答这个问题.
【拓展迁移】
(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 .知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.

在平面直角坐标系中, 是第一象限内一点,给出如下定义: 和 两个值中的最大值叫做点 的“倾斜系数” .
(1)求点 的“倾斜系数” 的值;
(2)①若点 的“倾斜系数” ,请写出 和 的数量关系,并说明理由;
②若点 的“倾斜系数” ,且 ,求 的长;
(3)如图,边长为 的正方形 沿直线 运动, 是正方形 上任意一点,且点 的“倾斜系数” ,请直接写出 的取值范围.

如图, 是 的外接圆, 是直径, ,连接 , , 与 相交于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

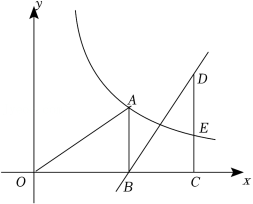
如图,点A在反比例函数 的图象上, 轴,垂足为 ,过 作 轴,交过 点的一次函数 的图象于D点,交反比例函数的图象于 点, .
(1)求反比例函数 和一次函数 的表达式;
(2)求 的长.