综合与实践
【问题情境】
数学活动课上,老师出示了一个问题:如图1,在正方形 中,E是BC的中点, , 与正方形的外角 的平分线交于 点.试猜想 与 的数量关系,并加以证明;
【思考尝试】
(1)同学们发现,取 的中点 ,连接 可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
【实践探究】
(2)希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 ,可以求出 的大小,请你思考并解答这个问题.
【拓展迁移】
(3)突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形 中, 为 边上一动点(点 不重合), 是等腰直角三角形, ,连接 .知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.

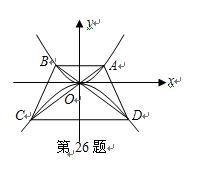
如图,点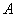 在抛物线
在抛物线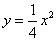 上,过点
上,过点 作与
作与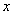 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点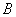 ,延长
,延长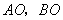 分别与抛物线
分别与抛物线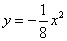 相交于点
相交于点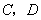 ,连接
,连接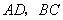 ,设点
,设点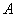 的横坐标为
的横坐标为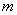 ,且
,且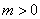 .
.
(1). 当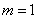 时,求点
时,求点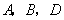 的坐标;
的坐标;
(2). 当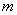 为何值时,四边形
为何值时,四边形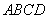 的两条对角线互相垂直;
的两条对角线互相垂直;
(3). 猜想线段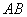 与
与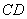 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
随着世界气候大会于2009年12月7-18日在丹麦首都哥本哈根的召开,“低碳”概念风靡全球。在“低碳”理念的引领下,某市为实现森林城市建设的目标,在今年春季的绿化工作中,绿化办计划为某住宅小区购买并种植400株树苗,某树苗公司提供如下信息:
信息一:可供选择的树苗有雪松、香樟,垂柳三种,并且要求购买雪松、香樟的数量相等。
信息二:如下表: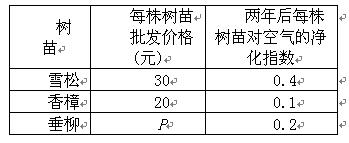
设购买雪松,垂柳分别为x株、y株。
(1). 写出y与x之间的函数关系式(不要求写出自变量的取值范围);
(2). 当每株垂柳的批发价P等于30元时,要使这400株树苗两年后对该住宅小区的空气净化指数不低于90,应怎样安排这三种树苗的购买数量,才能使购买树苗的总费用最低?最低的总费用是多少元?
(3). 当每株垂柳批发价格P(元)与购买数量y(株)之间存在关系P=30-0.05y时,求购买树苗的总费用W(元)与购买雪松数量x(株)之间的函数关系式(不要求写出自变量的取值范围),并求出购买树苗总费用的最大值。
如图,直线EF交⊙O于A、B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.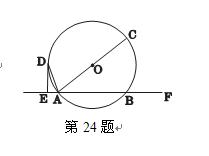
(1). 求证:AD平分∠CAE;
(2). 若DE=4cm,AE=2cm,求⊙O的面积。
供电局的电力维修工甲、乙两人要到45千米远的A地进行电力抢修.甲骑摩托车先行,t(t≥0)小时后乙开抢修车载着所需材料出发.
(1). 若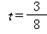 (小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(2). 若摩托车的速度是45千米/小时,抢修车的速度是60千米/小时,且乙不能比甲晚到,则t的最大值是多少?
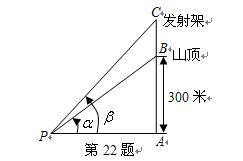
岳麓山风景名胜区系国家级重点风景名胜区,位于古城长沙湘江西岸。它的主峰海拔约为300米,主峰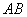 上建有一座电信信号发射架
上建有一座电信信号发射架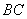 ,现在山脚
,现在山脚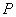 处测得峰顶的仰角为
处测得峰顶的仰角为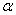 ,发射架顶端的仰角为
,发射架顶端的仰角为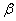 ,其中
,其中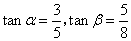 ,求发射架高
,求发射架高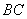 .
.