如图,四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为梯形,
为梯形, ,
, ,且
,且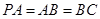 ,点
,点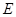 是棱
是棱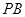 上的动点.
上的动点.
(Ⅰ)当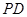 ∥平面
∥平面 时,确定点
时,确定点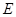 在
在 棱
棱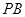 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角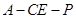 的余弦值.
的余弦值.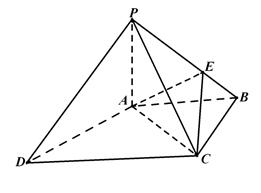
(12分)已知等差数列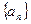 中,前n项和
中,前n项和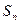 满足:
满足: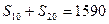 ,
,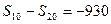 。
。
(Ⅰ)求数列的通项公式以及前n项和公式。
(Ⅱ)是否存在三角形同时具有以下两个性质,如果存在请求出相应的三角形三边
以及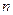 和
和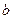 值:
值:
(1)三边是数列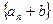 中的连续三项,其中
中的连续三项,其中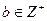 ;
;
(2)最小角是最大角的一半。
(8分)如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知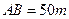 ,
,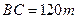 ,于A处测得水深
,于A处测得水深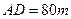 ,于B处测得水深
,于B处测得水深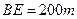 ,于C处测得水深
,于C处测得水深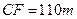 ,求∠DEF的余弦值。
,求∠DEF的余弦值。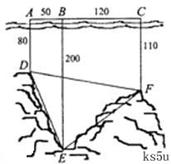
 |
(10分)已知函数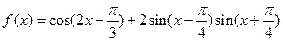
(Ⅰ)求函数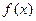 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(Ⅱ)求函数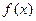 在区间
在区间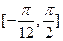 上的值域。
上的值域。
(10分)已知 <
< <
< <
<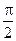 ,
,
(Ⅰ)求 的值.
的值.
(Ⅱ)求 .
.
(10分)在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
, .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.