)某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年) 的利润为500(1+
的利润为500(1+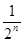 )万元(n为正
)万元(n为正 整数).
整数).
( Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为
Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为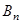 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求 、
、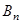 的表达式;
的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?