已知数列
的前
项和
，则其通项公式为
设函数
,其中
.
（1）当
时，求不等式
的解集；
（2）若不等式
的解集为
，求a的值.
已知函数
（1）若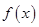
在区间［1，+∞）上是增函数，求实数a的取值范围；
（2）若x=-
是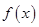的极值点，求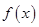在［1，a］上的最大值；
（3）在（2）的条件下，是否存在实数b，使得函数
=bx的图象与函数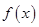的图象恰有3个交点，若存在，请求出实数b的取值范围；若不存在，试说明理由.
已知数列{an}满足a1＝1，an>0，Sn是数列{an}的前n项和，对任意的
n∈N*，有2Sn＝2an2＋an－1.
（1）求数列{an}的通项公式；
（2）记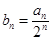
，求数列{bn}的前n项和Tn.
已知函数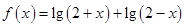
.
（1）求函数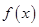
的定义域；
（2）若不等式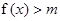
有解，求实数
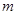的取值范围.
中，若
，那么
等于多少？