（ 10分）如图，已知点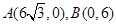
，经过A、B的直线
以每秒1个单位的速度向下作匀速平移运动，与此同时，点P从点B出发,在直线上以每秒1个单位的速度沿直线向右下方向作匀速运动．设它们运动的时间为
秒．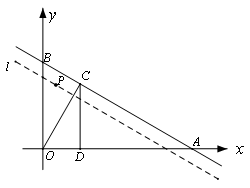
（1）用含
的代数式表示点P的坐标；（2）过O作OC⊥AB于C,过C作CD⊥
轴于D,问：为何值时,以P为圆心、1为半径的圆与直线OC相切？并说明此时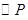
与直线CD的位置关系．
已知：如图，Rt⊿ABC和Rt⊿ADC，∠ABC=∠ADC=90°，点E是AC的中点.求证：∠EBD=∠EDB.
已知：如图，⊿ABC和⊿ADE都是等边三角形.求证：BD=CE．
解方程：
.
计算：
．
如图1，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA方向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s．连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．解答下列问题：
（1）当t为何值时，PQ∥BC．
（2）设△AQP面积为S（单位：cm2），当t为何值时，S取得最大值，并求出最大值．
（3）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．
（4）如图2，把△AQP沿AP翻折，得到四边形AQPQ′．那么是否存在某时刻t，使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由．