我们约定，若一个三角形（记为△A1）是由另一个三角形（记为△A）通过一次平移，或绕其任一边的中点旋转180°得到的，则称△A1是由△A复制的．以下的操作中每一个三角形只可以复制一次，复制过程可以一直进行下去．如图1，由△A复制出△A1，又由△A1复制出△A2，再由△A2复制出△A3，形成了一个大三角形，记作△B．以下各题中的复制均是由△A开始的，通过复制形成的多边形中的任意相邻两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．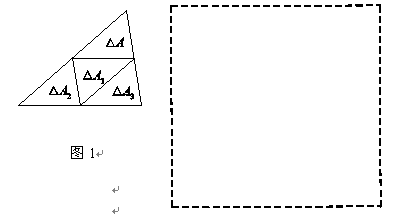
（1）图1中标出的是一种可能的复制结果，小明发现△A∽△B，其相似比为_________．在图1的基础上继续复制下去得到△C，若△C的一条边上恰有11个小三角形（指有一条边在该边上的小三角形），则△C中含有______个小三角形；
（2）若△A是正三角形，你认为通过复制能形成的正多边形是________；
（3）请你用两
次旋转和一次平移复制形成一个四
边形，在图2的方框内画出草图，并仿照图1作出标记．
如图，山脚下有一棵树AB，小华从点B沿山坡向上走50米到达点D，用 高为1.5米的测角仪CD测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB的高．（精确到0．1米）
（已知sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, sin15°≈0.26, cos15°≈0.97, tan15°≈0.27．）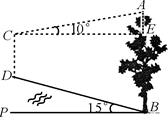
扬州市举办中学生足球赛，初中男子组共有市直学校的A、B两队和县区学校的e、f、g、h四队报名参赛，六支球队分成甲、乙两组，甲组由A、e、f三队组成，乙组由B、g、h三队组成，现要从甲、乙两组中各随机抽取一支球队进行首场比赛．
（1）在甲组中，首场比赛抽f 队的概率是；
（2）请你用画树状图或列表的方法，求首场比赛出场的两个队都是县区学校队的概率．
扬州市中学生骑电动车上学的现象越来越受到社会的关注．我市记者随机调查了一些家长对这种现象的态度（A：无所谓；B：反对；C：赞成），并将调査结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：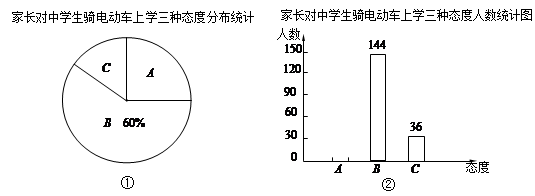
（1）在图①中，A部分所占扇形的圆心角度数为°；
（2）将图②补充完整；
（3）根据抽样调查结果，请你估计我市80000名中学生家长中有多少名家长持无所谓态度？
解不等式组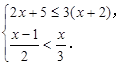
并写出它的整数解．
（1）计算：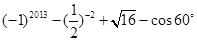
（2）化简：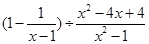
，请取一个合适的x的值再求上述代数式的值．