如图，虚线下方有足够大的场强大小E=5.0×103 V/m和上方场强为8mg/3q的匀强电场，方向均水平向右。质量均为m=1.5×10-2kg的A、B小球，其中B球为绝缘小球且不带电，被长为R的绝缘丝线悬挂在O点刚好静止在虚线上， A球带电荷量为qA=+6.0×10-6C，在竖直平面内的以某一初速度v竖直进入电场，运动到B点速度刚好水平，同时与B球发生正碰并立即粘在一起围绕O点做半径为R=0.7m完整的圆周运动，假设甲、乙两球可视为质点，g取10 m/s2。(sin53°=0.8,c0s53°=0.6)
（1）假设初速度v="20m/s" ，试求小球A与B球碰撞前能运动的水平位移的大小和整个过程中电场力对小球做功的最大值。
（2）如果小球刚好能做完整的圆周运动，试求碰撞前A球的最小速度和绳子所受的最大拉力分别多大。
如图所示，一轻质弹簧两端连着物体A和B，放在光滑的水平面上，物体A被水平速度为v0的子弹射中并且嵌入其中。已知物体B的质量为m，物体A的质量是物体B的质量的3/4，子弹的质量是物体B的质量的1/4
①求弹簧压缩到最短时B的速度。
②弹簧的最大弹性势能。
一半径为R的1/4球体放置在水平桌面上，球体由折射率为
的透明材料制成。如图所示，现有一束平行于桌面的光线射到球体表面上，折射入球体后再从竖直表面射出，已知入射光线与桌面的距离为R/2，求出射角θ。
一定质量的理想气体从状态A变化到状态B，再变化到状态C，其状态变化过程的p－V图象如图所示．已知该气体在状态A时的温度为27℃，求：
①该气体在状态B、C时的温度分别是多少？
②该气体从状态A到状态C的过程中内能的变化量是多少？
③该气体从状态A到状态C的过程中是吸热还是放热？传递的热量是多少？
如图所示，一对磁偏转线圈形成的匀强磁场分布在R = 0.10m的圆形区域内,磁感应强度为0.1T。圆的左端跟y轴相切于直角坐标系的原点O，右端跟足够大的荧光屏MN相切于x轴上A点，置于原点的粒子源沿x轴正方向射出带正电的粒子流，以v =
×106m/s射入磁场，粒子的比荷为1×108c/kg，重力不计。求
（1）粒子在磁场中运动的时间。
（2）粒子打在荧光屏上的位置距A的距离。
（3）要使粒子打不到荧光屏上，求粒子的速度大小应满足的条件。
质量为3㎏的长木板A置于光滑的水平地面上，质量为2㎏木块B（可视为质点）置于木板A的左端，在水平向右的力F作用下由静止开始运动，如图甲所示。A、B运动的加速度随时间变化的图象如图乙所示。（g取10m/s2）求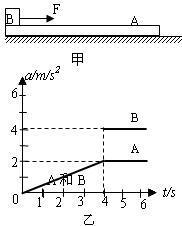
（1）木板与木块之间的动摩擦因数。（设最大静摩擦力等于滑动摩擦力）。
（2）4s末A、B的速度。
（3）若6s末木板和木块刚好分离，则木板的长度为多少？