（本小题满分12分）
设函数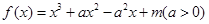
．
（1）若函数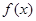
在
内没有极值点，求实数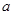
的取值范围；
（2）
时函数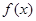有三个互不相同的零点，求实数
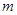的取值范围；
（3）若对任意的
，不等式
在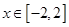
上恒成立，求实数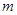的取值范围．
（本小题满分12分）带有编号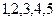
的五个球
（1）全部投入4个不同的盒子里，有多少种不同的方法？
（2）放进4个不同的盒子里，每盒一个，有多少种不同的方法？
（3）将其中的4个球投入4个盒子里的一个（另一球不投入），有多少种不同的方法？
（4）全部投入4个不同的盒子里，没有空盒，有多少种不同的放法？
（本小题满分12分）已知二阶矩阵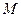
有特征值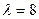
及对应的一个特征向量
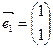，并且矩阵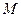对应的变换将点（-1，2）变换成（-2，4）.
（1）求矩阵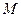
（2）求矩阵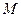的另一个特征值及对应的一个特征向量
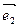的坐标之间关系
（3）求直线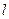
：
在矩阵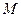的作用下的直线
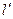的方程
（本小题满分12分）已知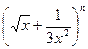
的第五项的二项式系数与第三项的二项式系数的比是14:3，求展开式中的常数项.
函数f(x)＝x3＋3ax2＋3bx＋c在x＝2处有极值，其图象在x＝1处的切线平行于直线3x＋y＋2＝0．
（1）求a，b的值； （2）求函数的极大值与极小值的差．
已知函数
的最小正周期为
（1）求
的值；（2）求函数f(x)的单调递增区间；
（3）求函数f(x)在区间[0，
]上的取值范围．