选修4-4:坐标系与参数方程
已知平面直角坐标系 中,以
中,以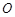 为极点,
为极点, 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线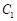 方程为
方程为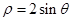 .
. 的参数方程为
的参数方程为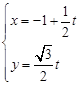 (
( 为参数).
为参数).
(Ⅰ)写出曲线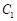 的直角坐标方程和
的直角坐标方程和 的普通方程;
的普通方程;
(Ⅱ)设点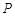 为曲线
为曲线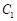 上的任意一点,求点
上的任意一点,求点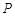 到曲线
到曲线 距离的取值范围.
距离的取值范围.
已知函数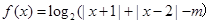 .
.
(Ⅰ)当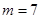 时,求函数
时,求函数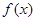 的定义域;
的定义域;
(2)若关于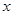 的不等式
的不等式 的解集是
的解集是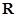 ,求
,求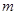 的取值范围.
的取值范围.
知椭圆
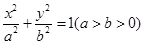 的离心率为
的离心率为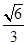 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 ,直线l的方程为:
,直线l的方程为: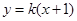
(Ⅰ)求椭圆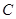 的方程;
的方程;
(Ⅱ)已知直线l与椭圆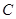 相交于
相交于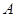 、
、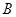 两点
两点
①若线段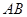 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率 的值;
的值;
②已知点 ,求证:
,求证: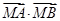 为定值
为定值
如图,F1,F2分别是椭圆C: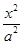 +
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°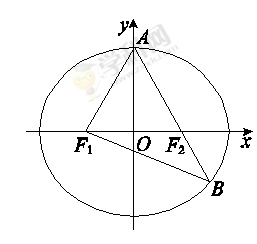
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40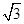 ,求a,b的值
,求a,b的值
设函数f(x)=x|x-a|+b,求证:f(x)为奇函数的充要条件是a2+b2=0.
以下茎叶图记录了甲组3名同学寒假假期中去图书馆 学习的次数和乙组4名同学寒假假期中去图书馆
学习的次数和乙组4名同学寒假假期中去图书馆 学习的次数.乙组记录中有一个数据模糊,无法确认,在图中以
学习的次数.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
(Ⅰ)如果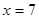 ,求乙组同学去图书馆学习次数的平均数和方差;
,求乙组同学去图书馆学习次数的平均数和方差;
(Ⅱ)如果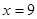 ,从学习次数大于8的学生中选两名同学,求选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率.
,从学习次数大于8的学生中选两名同学,求选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率.