已知函数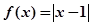
.
（1）用分段函数的形式表示该函数；
（2）在右边所给的坐标系中画出该函数的图象；
（3）写出该函数的定义域、值域、奇偶性、单调区间(不要求证明).
将一枚骰子（形状为正方体，六个面上分别标有数字1，2，3，4，5，6的玩具）先后抛掷两次，骰子向上的点数依次为
．
（1）求
的概率；
（2）求
的概率P；
（3）试将右侧求⑵中概率P的伪代码补充完整．
设点A为单位圆上一定点，求下列事件发生的概率：
（1）在该圆上任取一点B，使AB间劣弧长不超过
；
（2）在该圆上任取一点B，使弦AB的长度不超过
。
已知直线
与椭圆
相交于A、B两点.。
（1）若椭圆的离心率为
，焦距为2，求线段AB的长；
（2）若向量
与向量
互相垂直（其中O为坐标原点），当椭圆的离心率e=2时，求椭圆的长轴的长.
.如图，在四棱锥S-ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，E、F分别是AB、SC的中点。
(Ⅰ)求证：EF∥平面SAD；
(Ⅱ)设SD = 2CD，求二面角A－EF－D的大小；
已知抛物线C：
，过C上一点M，且与M处的切线垂直的直线称为C在点M的法线．若C在点M的法线的斜率为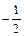
，求点M的坐标（x0，y0）；