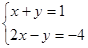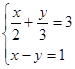．如图，将腰长为的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限，其中点A在y轴上，点B在抛物线y＝ax2＋ax－2上，点C的坐标为(－1，0)．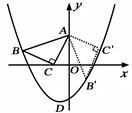
(1)点A的坐标为 ，点B的坐标为 ；
(2)抛物线的关系式为 ，其顶点坐标为 ；
(3)将三角板ABC绕顶点A逆时针方向旋转90°，到达
的位置．请判断点
、
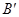是否在(2)中的抛物线上，并说明理由．
一个口袋中有10个红球和若干个白球。从口袋中随机摸出一球，记下其颜色，再把它放回口袋中，不断重复上述过程，实验中总共摸了200次，其中有50次摸到红球。问：口袋中白球有几个？
如图已知∠C=∠A，∠B=∠E，点D为CA的中点，说明下列判断成立的理由。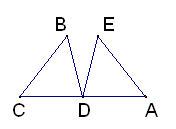
△BDC≌△EDA
CB=AE
如图，在正方形网格上有一个△ABC把△ABC向上平移3小方格，作出平移后的图形；
作AB边上的高CD和BC边上的中线AE（不写作法）
若网格上的最小正方形边长为1，求△ABC的面积.
在下面解题过程中的横线上填空，并在括号内注明理由。（每空1分）
如图，已知∠B =∠C，AD = AE，说明DB与EC相等。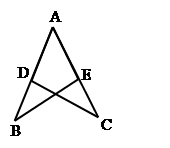
解：在△ABE和△ACD中
∠B = _______（已知）
∠A = _______（）
AD =" AE" （已知）
∴△ABE ≌△ACD （）
∴AB = _______（）
又∵AD = AE
∴AB－AD＝AC－AE，
即DB = EC．
解下列方程组
