(本题10分)在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.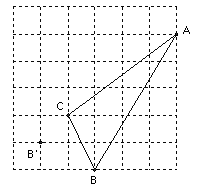
(1)过点B′画出平移后的△A′B′C′,使A′和A、B′和B、C′和C分别对应;
(2)若连接AA′、BB′、CC′,则这三条线段之间的关系是______,仔细观察,图中互相平行的线段共有对;
(3)求△A′B′C′的面积.
(本题8分)先化简,再求值: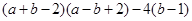 ,其中
,其中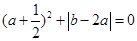 .
.
(本题8分)如图,MN//EF,GH//EF,BA⊥CA于点A,若∠1=70º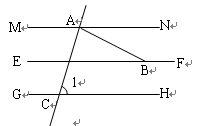
求:∠ABF的度数.
分解因式:(每小题4分,共8分)
(1)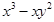 (2)
(2)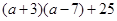
(12分)如图(1),点A、B、C在同一直线上,且△ABE, △BCD都是等边三角形,连结AD,CE.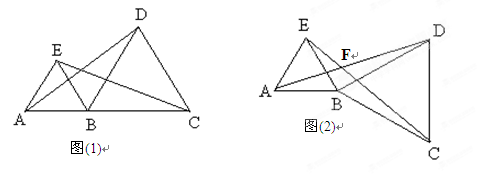
(1)△BEC可由△ABD顺时针旋转得到吗?若是,请描述这一旋转变换过程;若不是,请说明理由;
(2)若△BCD绕点B顺时针旋转,使点A,B,C不在同一直线上(如图(2)),则在旋转过程中:
①线段AD与EC的长度相等吗?请说明理由.
②锐角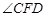 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出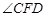 的度数;若改变,请说明理由.
的度数;若改变,请说明理由.
(注:等边三角形的三条边都相等,三个角都是60°)