(12分)如图(1),点A、B、C在同一直线上,且△ABE, △BCD都是等边三角形,连结AD,CE.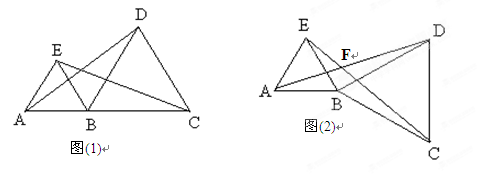
(1)△BEC可由△ABD顺时针旋转得到吗?若是,请描述这一旋转变换过程;若不是,请说明理由;
(2)若△BCD绕点B顺时针旋转,使点A,B,C不在同一直线上(如图(2)),则在旋转过程中:
①线段AD与EC的长度相等吗?请说明理由.
②锐角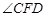 的度数是否改变?若不变,请求出
的度数是否改变?若不变,请求出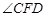 的度数;若改变,请说明理由.
的度数;若改变,请说明理由.
(注:等边三角形的三条边都相等,三个角都是60°)
已知AB∥CD,BE、CF平分∠ABC,∠BCD.探索BE与CF的位置关系,并说明理由.
乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 (用式子表达).
先化简,再求值(m﹣2n)(m+2n)﹣ ,其中m=
,其中m= ,n=﹣1.
,n=﹣1.
阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,D为BC中点,E、F分别为AB、AC上一点,且ED⊥DF,
求证:BE+CF>EF.
小明发现,延长FD到点H,使DH=FD,连结BH、EH,构造△BDH和△EFH,通过证明△BDH与△CDF全等、△EFH为等腰三角形,利用△BEH使问题得以解决(如图2).
参考小明思考问题的方法,解决问题:
如图3,在矩形ABCD中,O为对角线AC中点,将矩形ABCD翻折,使点B恰好与点O重合,EF为折痕,猜想EF、BE、FC之间的数量关系?并证明你的猜想.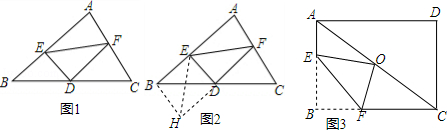
在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线l:y=kx+3.
(1)当直线l经过D点时,求点D的坐标及k的值;
(2)当直线l与正方形有两个交点时,直接写出k的取值范围.