阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,D为BC中点,E、F分别为AB、AC上一点,且ED⊥DF,
求证:BE+CF>EF.
小明发现,延长FD到点H,使DH=FD,连结BH、EH,构造△BDH和△EFH,通过证明△BDH与△CDF全等、△EFH为等腰三角形,利用△BEH使问题得以解决(如图2).
参考小明思考问题的方法,解决问题:
如图3,在矩形ABCD中,O为对角线AC中点,将矩形ABCD翻折,使点B恰好与点O重合,EF为折痕,猜想EF、BE、FC之间的数量关系?并证明你的猜想.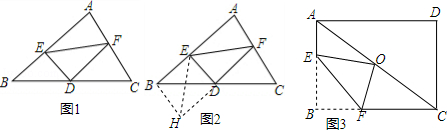
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)若弧AE=弧DE,DF=2,求弧AD的长.
(1)如图:靠着22 m长的房屋后墙,围一块150 m2的矩形鸡场,现在有篱笆共40 m。求矩形的长、宽各多少米?
(2)若把“围一块150 m2的矩形鸡场”改为“围一块S m2的矩形鸡场”,其它条件不变,能否使S最大。若能,请你求出此时矩形的长、宽及最大面积;若不能,请你说明理由。
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上。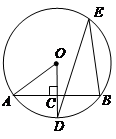
(1)若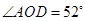 ,求
,求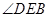 的度数;
的度数;
 (2)若
(2)若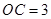 ,
,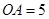 ,求
,求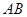 的长.
的长.
一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.(1)求摸出1个球是白球的概率;(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为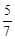 ,求n的值.
,求n的值.
如图,方格纸中的每个小方格都是正方形,△ABC的顶点均在格点上,建立平面直角坐标系.(1)以原点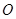 为对称中心,画出与△ABC关于原点
为对称中心,画出与△ABC关于原点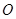 对称的△A1B1C1,并写出A1 的坐标。(2)将原来的△ABC绕着点B顺时针旋转90°得到△A2B2C2,试在平面直角坐标系中画出△A2B2C2。
对称的△A1B1C1,并写出A1 的坐标。(2)将原来的△ABC绕着点B顺时针旋转90°得到△A2B2C2,试在平面直角坐标系中画出△A2B2C2。