(本小题满分12分)某班同学到野外活动,为测量一池塘两端A、B的距离,设计了几种方案,下面介绍两种:(I)如图(1),先在平地取一个可以直接到达A、B的点C,并分别延长AC到D,BC到E,使DC=AC,BC=EC,最后测出DE的距离即为AB的长。(II)如图(2),先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离。阅读后回答下列问题:
(1)方案(I)是否可行?为什么?
(2)方案(II)是否切实可行?为什么?
(3)方案(II)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°,方案(II)是否成立?
(4)方案(II)中,若使BC=n·CD,能否测得(或求出)AB的长?理由是 ,若ED=m,则AB= 。
某质检部门抽取甲、乙两厂相同数量的产品进行质量检测,测得甲厂有合格品48件,乙厂有合格品45件,且甲厂的产品合格率比乙厂的产品合格率高5%,问甲厂产品的合格率是多少?
如图,△ABC与△ADE关于直线MN对称.BC与DE的交点F在直线MN上.
①指出两个三角形中的对称点;
②指出图中相等的线段和角;
③图中还有对称的三角形吗?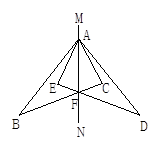
如图所示,(1)在图a中把正方形分成四个全等的三角形;(2)在图b中把正五边形分成五个全等的三角形;(3)在图c中把正六边形分成六个全等的三角形?(4)通过(1)(2)(3)的解答,你发现了什么?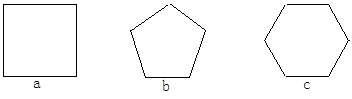
连一连:
(1)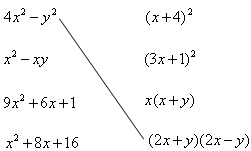
(2)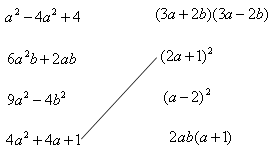
18、已知a+b=2,求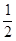 a2+ab+
a2+ab+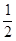 b2的值.
b2的值.