(本题6分)已知正比例函数过点(-1,2),求此函数的解析式,并画出函数图象
解下列不等式(组)并把解集表示在数轴上。(1)
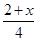 ≥
≥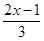 ;
; (2)
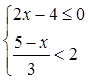
(6分)如图已知三角形 AB
AB C的三个顶点坐标分别是A(0,1),B(
C的三个顶点坐标分别是A(0,1),B( 3,4),C(3,0),请你在直角坐标系中作出三角形ABC ,并作出它关于X轴对称的图形。
3,4),C(3,0),请你在直角坐标系中作出三角形ABC ,并作出它关于X轴对称的图形。


小明每天早上要在7:50之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,10分后,小明和爸爸都发现她忘了带语文书 。于是,小明以80米/分的速度返回,小明爸爸立
。于是,小明以80米/分的速度返回,小明爸爸立 即以120米/分的速度去送书给小明,并且在途中碰上了她。
即以120米/分的速度去送书给小明,并且在途中碰上了她。(1)爸爸送书给小明用
 了几分钟?
了几分钟?(2)小明这天早上几点出
 发才不会迟到?(精确到分钟)
发才不会迟到?(精确到分钟)
某校开展植树活动,七(1) 27人,七(2) 19人,现另调26人去支援,使七(1)是七(2)的2倍,问应调往七(1)、七(2)各多少人?