.(本小题满分7分)已知:正方形 中,
中, ,
, 绕点
绕点 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交 (或它们的延长线)于点
(或它们的延长线)于点
 .当
.当 绕点
绕点 旋转到
旋转到 时(如图1),易证
时(如图1),易证 .
.(1)当
 绕点
绕点 旋转到
旋转到 时(如图2),线段
时(如图2),线段 和
和 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.(2)当
 绕点
绕点 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段 和
和 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
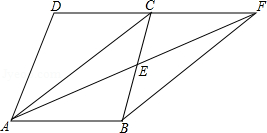
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且 .
(1)求证:直线MN是⊙O的切线;
(2)若 , ,求⊙O的半径.
张家界到长沙的距离约为320km,小明开着大货车,小华开着小轿车,都从张家界同时去长沙,已知小轿车的速度是大货车的1.25倍,小华比小明提前1小时到达长沙.试问:大货车和小轿车的速度各是多少?
如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度 ,求旗杆AB的高度(结果精确到0.1米).参考数据: .

求不等式组 的解集,并把它们的解集在数轴上表示出来.
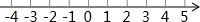
已知:如图,在四边形ABCD中, ,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.