如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-4,0),点N的坐标为(-3,-2),直角梯形OMNH关于原点O的中心对称图形是直角梯形OABC,(点M的对应点为A, 点N的对应点为B, 点H的对应点为C);
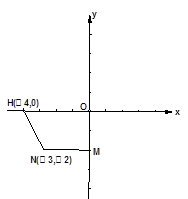
求出过A,B,C三点的抛物线的表达式
在直角梯形OABC中,截取BE=AF=OG=m(m>0),且E,F,G分别在线段BA,AO,OC上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
在(2)的情况下,是否存在BG∥EF的情况,若存在,请求出相应m的值,若不存在,说明理由.
(2014年江苏淮安14分)如图1,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
(1)当t= 时,△PQR的边QR经过点B;
(2)设△PQR和矩形OABC重叠部分的面积为S,求S关于t的函数关系式;
(3)如图2,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,求t的值.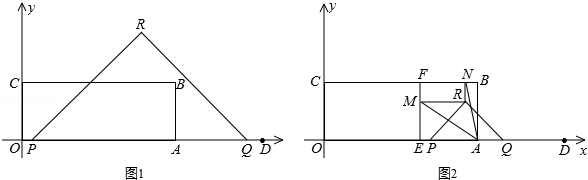
(2014年吉林省10分)如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=6cm,BD=8cm,动点P,Q分别从点B,D同时出发,运动速度均为1cm/s,点P沿B→C→D运动,到点D停止,点Q沿D→O→B运动,到点O停止1s后继续运动,到B停止,连接AP,AQ,PQ.设△APQ的面积为y(cm2)(这里规定:线段是面积0的几何图形),点P的运动时间为x(s).
(1)填空:AB= cm,AB与CD之间的距离为 cm;
(2)当4≤x≤10时,求y与x之间的函数解析式;
(3)直接写出在整个运动过程中,使PQ与菱形ABCD一边平行的所有x的值.
(年湖南郴州10分)如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).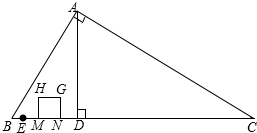
(1)当t为何值时,点G刚好落在线段AD上?
(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.
(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?
(年黑龙江绥化10分)如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.
(年黑龙江牡丹江农垦10分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.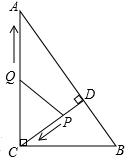
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?