如图,已知直线y=-2x+4与x轴、y轴分别相交于A、C两点,抛物线
y=-2x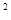 +bx+c (a≠0)经过点A、C.
+bx+c (a≠0)经过点A、C.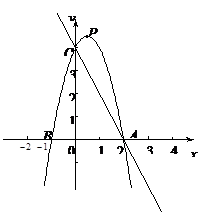
求抛物线的解析式;
设抛物线的顶点为P,在抛物线上存在点Q,使△ABQ的面积等于△APC面积的4倍.求出点Q的坐标;
点M是直线y=-2x+4上的动点,过点M作ME垂直x轴于点E,在y轴(原点除外)上是否存在点F,使△MEF为等腰直角三角形? 若存在,求出点F的坐标及对应的点M的坐标;若不存在,请说明理由
解方程:
(1)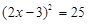 ;(2)
;(2)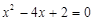 ;(3)x2-5x-6=0.
;(3)x2-5x-6=0.
如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,
连接AM、CM.其中BN=BM,∠MBN=60°,连接EN
(1)证明:△ABM≌△EBN
(2)当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为 时,求正方形的边长.
时,求正方形的边长.
如图,在四边形 中,
中, ,
, ,
, ,
, ,
, 是
是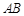 中点,
中点, 是
是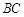 中点,且
中点,且 ,求梯形
,求梯形 的面积.
的面积.
如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.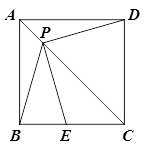
(1)求证:PE="PD" ;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
如图,菱形ABCD,对角线AC、BD交于点O,DE//AC,CE//BD,求证:OE=BC