根据我省“十二五”铁路规划,连云港至徐州客运专线项目建成后,连云港至徐州的最短客运时间将由现在的2小时18分钟缩短为36分钟,其速度每小时将提高260km,求提速后的火车速度.(精确到1km/h)
为开发农业生态发展,王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活率98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.分别计算甲、乙两山样本的极差;
分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
试通过计算说明,哪个山上的杨梅产量较稳定?

解下列一元二次方程: x2+2x-2=0
(x+1)(x-3)=-4

已知:如图,⊙O1与坐标轴交于A(1,0)、B(5,0)两点,点O1的纵坐标为 .求⊙O1的半径.
.求⊙O1的半径.
已知:如图,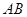 为
为 的直径,
的直径, 交
交 于点
于点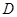 ,
, 交
交 于点
于点 .
.
(1)求 的度数;
的度数;
(2)求证: .
.
如图,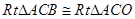 ,点
,点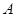 在第二象限内,点
在第二象限内,点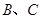 在
在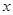 轴的负半轴上,
轴的负半轴上,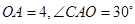 .
.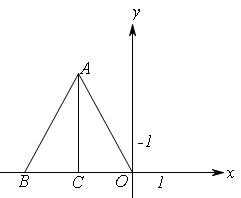
⑴求点
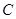 的坐标;
的坐标;⑵如图,将
 绕点
绕点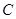 按顺时针方向旋转
按顺时针方向旋转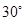 到
到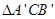 的位置,其中
的位置,其中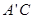 交直线
交直线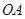 于点
于点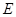 ,
,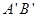 分别交直线
分别交直线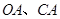 于点
于点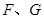 ,则除
,则除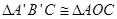 外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);
外,还有哪几对全等的三角形,请直接写出答案(不再另外添加辅助线);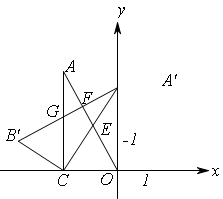
⑶在⑵的基础上,将
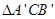 绕点
绕点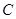 按顺时针方向继续旋转,当
按顺时针方向继续旋转,当 的面积为
的面积为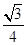 时,求直线
时,求直线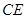 的函数表达式.
的函数表达式.