阅读填空题
已知:如图,DC⊥CA,EA⊥CA,DB⊥EB,DB=BE,求证:△BCD与△EAB全等.
证明:∵DC⊥CA,EA⊥CA,DB⊥EB (已知)
∴∠C=∠A=∠DBE=90( )
∵∠DBC+∠EBA+∠DBE=180°
∴∠DBC+∠EBA=90°
又∵在直角△BCD中,∠DBC+∠D=90°( )
∴∠D=∠EBA ( )
在△BCD与△EAB中, ∠D=∠EBA(已证)
∠D=∠EBA(已证)
∠C= (已证)
DB= (已知)
∴△BCD≌△EAB( )
(本题6分)如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。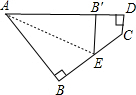
(1)试判断B'E与DC的位置关系并说明理由;
(2)如果∠C=130°,求∠AEB的度数。
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.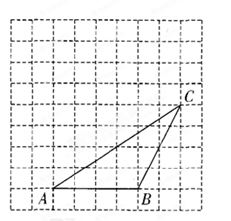
(1)请在图中画出平移后的△A´B´C´,
(2)再在图中画出△ABC的高CD,
(3)在右图中能使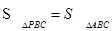 的格点P的个数有 个(点P异于A).
的格点P的个数有 个(点P异于A).
(本题4分)先化简,再求值:(3+4x)(3-4x)+(3-4x)2,其中x=
因式分解(每小题3分,共6分)
(1)4a2-16
(2)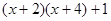
如图,在平面直角坐标系中,直线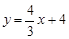 分别交
分别交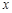 轴,
轴, 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作 ,垂足为H,连接NP.设点P的运动时间为t秒.
,垂足为H,连接NP.设点P的运动时间为t秒.
① 若△NPH的面积为1,求t的值;
② 点Q是点B关于点A的对称点,问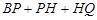 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.