如图,在平面直角坐标系中,直线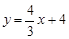 分别交
分别交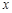 轴,
轴, 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作 ,垂足为H,连接NP.设点P的运动时间为t秒.
,垂足为H,连接NP.设点P的运动时间为t秒.
① 若△NPH的面积为1,求t的值;
② 点Q是点B关于点A的对称点,问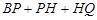 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
(本题10分)解方程:
(1)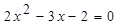
(2)解方程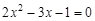 (用配方法)
(用配方法)
李强靠勤工俭学的收入维持上大学的费用.下面是他某一周的收支情况表(收入为正,支出为负,单位为元)
| 周一 |
周二 |
三 |
四 |
五 |
六 |
日 |
| +15 |
+10 |
0 |
+20 |
+15 |
+10 |
+14 |
| -8 |
-12 |
-19 |
-10 |
-9 |
-11 |
-8 |
(1)到这个周末,李强有多少节余?
(2)照这样,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
学习有理数得乘法后,老师给同学们这样一道题目:计算:49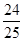 ×(-5),看谁算的又快又对,有两位同学的解法如下:
×(-5),看谁算的又快又对,有两位同学的解法如下:
小明:原式=-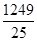 ×5=-
×5=-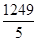 =-249
=-249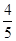 ;
;
小军:原式=(49+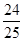 )×(-5)=49×(-5)+
)×(-5)=49×(-5)+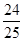 ×(-5)=-249
×(-5)=-249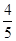 ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19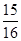 ×(-8)
×(-8)
一只小狗从某地出发在一直线上来回跑,假定向右跑记为为正数,向左跑记为负数,记录小狗跑动的各段路程依次为(单位:米):+5,-3,+10,-8,-6,+12,-10.求:
(1)小狗最后是否回到出发点?
(2)在跑动过程中,如果每跑动1米奖励小狗2粒狗粮,则小狗一共得到多少粒狗粮?
(1)画出数轴,并用数轴上的点表示下列各数:
-5,2.5,3,-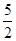 ,0,-3,3
,0,-3,3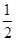 .
.
(2)用“<”号把各数从小到大连起来: