一个不透明的口袋中装有红、黄、绿三种颜色的小球（它们除颜色不同外其余都相同），其中红球2个，黄球1个，从中任意摸出1球是红球的概率是
．求口袋中绿球的个数；
第一次从袋中任意摸出1球（不放回），第二次再任意摸出1球，请你用画树状图或列表的方法表示所有等可能的结果，并求两次都摸到红球的概率．
一个几何体的三视图如图所示，它的俯视图为菱形请写出该几何体的形状，并根据图中所给的数据求出它的侧面积
已知a=-2，b=1，求
的值
如图，在平面直角坐标系xOy中，抛物线y＝ax2＋bx＋3的顶点为M（2，－1），交x轴于A、B两点，交y轴于点C，其中点B的坐标为（3，0）。
（1）求该抛物线的解析式；
（2）设经过点C的直线与该抛物线的另一个交点为D，且直线CD和直线CA关于直线BC对称，求直线CD的解析式；
（3）在该抛物线的对称轴上存在点P，满足PM2＋PB2＋PC2＝35，求点P的坐标；并直接写出此时直线OP与该抛物线交点的个数。
如图，在边长为2的等边△ABC中，AD⊥BC,点P为边AB 上一个动点，过P点作PF//AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.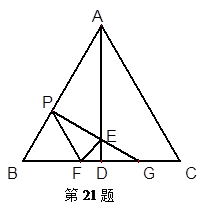
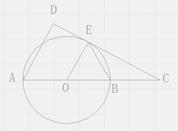
（1）①填空：如果BP=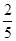
,则BG=;
②用x的代数式表示线段DG的长,并直接写出自变量x的取值范围;
（2）记△DEF的面积为S,求S与x之间的函数关系式。
（3）当以P、E、F为顶点的三角形与△EDG相似时，请求出BP的长。
如图，AB是⊙O的直径，C是AB延长线上一点，CD与⊙O相切于点E，AD⊥CD。
（1）求证：AE平分∠DAC；
（2）若AB=6，∠ABE=60°，①求AD的长；②求出图中阴影部分的面积。