如图所示,在粗糙水平地面上放置一光滑的斜面(斜面足够长),斜面的倾角为37°。在水平地面上有A、B两点,A、B之间的距离为4m,斜面与地面上的B点相接。在A点放一个可以视为质点的物体P,已知P与地面的动摩擦因数为0.2。让物体P以5m/s的速度由A点向右运动。(g=10m/s2,sin37°=0.6,cos37°=0.8)
求:
在整个运动过程中,物体P在斜面上运动的时间。
物体P最终的位置。
用长L=1.6m的细绳,一端系着质量M=1kg的木块,另一端挂在固定点上。现有一颗质量m=20g的子弹以v1=500m/s的水平速度向木块中心射击,结果子弹穿出木块后以v2=100m/s的速度前进。问木块能运动到多高?(取g=10m/s2,空气阻力不计)
一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多),圆管中有两个直径与细管内径相同的小球(可视为质点)。A球的质量为m1, B球的质量为m2。它们沿环形圆管顺时针运动,经过最低点时的速度都为v0。设A球运动到最低点时,球恰好运动到最高点,若要此时两球作用于圆管的合力为零,那么m1,m2,R与v0应满足关系式是。
如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R="5.0" m,轨道在C处与水平地面相切.在C处放一小物块,给它一水平向左的初速度vo="5" m/s,结果它沿CBA运动,通过A点,最后落在水平面上的D点,求C、D间的距离s.g="10" m/s2.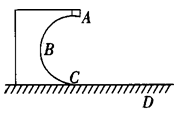
在勇气号火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来.假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为v0,求它第二次落到火星表面时速度的大小,计算时不计火星大气阻力.已知火星的一个卫星的圆轨道的半径为r,周期为T.火星可视为半径为r0的均匀球体.
水平放置的水管,距地面高h=1.8m,管内横截面积S=2.00m2.有水从管口处以不变的速度v=2.0m/s源源不断地沿水平方向射出,设出口处横截面上各处水的速度都相同,并假设水流在空中不散开.取重力加速度g=10m/s2,不计空气阻力.求水流稳定后在空中有多少立方米的水.