如图所示,三根轻线结于O点,并分别与套环A、B和重物C连接,A、B环重均为50N,套在水平横杆上,C重为120N,AO与BO两线等长并与横杆的夹角均为37°,整个系统处于静止状态,(sin37°=0.6,cos37°=0.8)求:

AO与BO两线中的张力大小;
A环所受杆的弹力与摩擦力的大小;
若将B点向左移一点后系统仍处于静止状态,与原来相比,A环所受线的拉力、杆的支持力和摩擦力大小分别如何变化?
如图13所示,有一磁感强度 的水平匀强磁场,垂直放置一很长的金属框架,框架上有一导体
的水平匀强磁场,垂直放置一很长的金属框架,框架上有一导体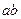 与框架边垂直且始终保持良好接触,由静止开始下滑。已知框架的宽度为
与框架边垂直且始终保持良好接触,由静止开始下滑。已知框架的宽度为 ,质量为
,质量为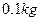 ,电阻为
,电阻为 ,框架电阻不计,取
,框架电阻不计,取 ,求:
,求:
(1) 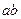 中电流的方向如何?
中电流的方向如何?
(2)导体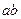 下落的最大速度;
下落的最大速度;
(3)导体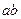 在最大速度时的电功率。
在最大速度时的电功率。
(10分)如图12所示,在 轴上方有匀强磁场
轴上方有匀强磁场 ,一个质量为
,一个质量为 ,带电量为
,带电量为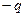 的的粒子,以速度
的的粒子,以速度 从
从 点以
点以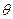 角射入磁场,粒子重力不计,求:
角射入磁场,粒子重力不计,求:
(1)粒子在磁场中的运动时间.
(2)粒子离开磁场的位置.
如图所示,竖直放置的正对平行金属板长L,板间距离也为L,两板间有场强为E的匀强电场(电场仅限于两板之间),右极板的下端刚好处在一有界匀强磁场的边界(虚线所示)上,该边界与水平成45°夹角,边 界线以右有垂直纸面向里的匀强磁场。一质量为m、电量为e的电子在左侧金属板的中点从静止开始,在电场力作用下加速向右运动,穿过右极板中心小孔后,进入匀强磁场。求:
界线以右有垂直纸面向里的匀强磁场。一质量为m、电量为e的电子在左侧金属板的中点从静止开始,在电场力作用下加速向右运动,穿过右极板中心小孔后,进入匀强磁场。求:
(1)从电子开始运动到进入匀强磁场所需的时间;
(2)匀强磁场的磁感应强度B应满足什么条件,才能保证电子从磁场出来后,还能穿越平行金属板间的电场区域。
如图所示,一小球从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后,进入半径 的光滑竖直圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度
的光滑竖直圆形轨道,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度 ,水平距离
,水平距离 ,水平轨道AB长为
,水平轨道AB长为 .小球与水平轨道间的动摩擦因数
.小球与水平轨道间的动摩擦因数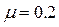 ,重力加速度
,重力加速度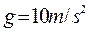 .则:
.则:
(1)若小球恰能通过圆形轨道的最高点,求小球在A点的初速度?
(2)若小球既能通过圆形轨道的最高点,又不掉进壕沟,求小球在A点的初速度的范围是多少?
如图所示,小球B用轻绳悬挂于O点,球B恰好与水平地面D点接触,水平地面与斜面连接处E可视为一小段圆弧,水平地面DE部分长度L=3.5m。一质量为m的滑块A(可视为质点)从倾角370、高度h =3m的斜面上C点由静止释放,并在水平面上与B球发生弹性碰撞。已知滑块A与接触面的动摩擦因数均是μ = 0.2,O点与C点在同一水平面上,小球B与滑块A质量相等(sin370=0.6,cos370=0.8,g = 10m/s2)。试求:
(1)B球与A球第一次碰撞后,A球摆动的最大偏角;
(2)B球第1次回到斜面上的高度;
(3)B球最终的位置到E处的距离。