如图所示在直角梯形OABC中
点M是棱SB的中点,N是OC上的点,且ON:NC=1:3。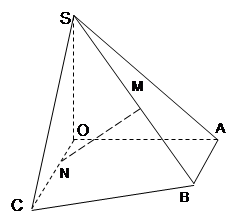
(1)求异面直线MM与BC所成的角;
(2)求MN与面SAB所成的角.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.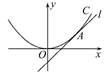
(1)求实数b的值.
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.
已知直线y=-2上有一个动点Q,过点Q作直线l1垂直于x轴,动点P在l1上,且满足OP⊥OQ(O为坐标原点),记点P的轨迹为C.
(1)求曲线C的方程.
(2)若直线l2是曲线C的一条切线,当点(0,2)到直线l2的距离最短时,求直线l2的方程.
椭圆C1: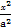 +
+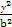 =1(a>b>0)的左、右顶点分别为A,B,点P是双曲线C2:
=1(a>b>0)的左、右顶点分别为A,B,点P是双曲线C2: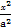 -
-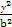 =1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D点,若S△ACD=S△PCD.
=1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D点,若S△ACD=S△PCD.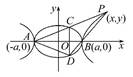
(1)求P点的坐标.
(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率;若不能,请说明理由.
P(x0,y0)(x0≠±a)是双曲线E: -
- =1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为
=1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为 .
.
(1)求双曲线的离心率.
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足 =λ
=λ +
+ ,求λ的值.
,求λ的值.
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为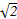 ,且过点P(4,-
,且过点P(4,-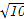 ).
).
(1)求双曲线的方程.
(2)若点M(3,m)在双曲线上,求证: ·
·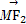 =0.
=0.
(3)求△F1MF2的面积.