已知平面向
量
，
，
，其中
，且函数
的图象过点
．
（1）求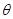
的值；
(2) 将函数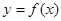
图象上各点的横坐标变为原来的的2倍，纵坐标不变，得到函数
的图象，求函数在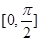
上的最大值和最小值．
（本大题满分14分）
如图，某公园摩天轮的半径为40ｍ，圆心O距地面的高度为50ｍ，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处
（1）已知在时刻
（min）时点P距离地面的高度
，求2006min时点P距离地面的高度；
（2）当离地面（50+20
）m以上时，可以看到公园的全貌，求转一圈有多少时间可以看到公园全貌？
（本题13分）
已知函数
，
（1）用五点法画出它在一个
周期内的闭区间上的图象；
（2）说明此函数图象可由
，的图象经怎样的变换得到.
（本题13分）
设两个非零向量a与b不共线，
（1）若向量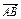
=a+b,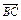
=2a+8b,
=3(a-b)，求证：A、B、D三点共线；
（2）试确定实数k，使向量ka+b和向量a+kb共线.
（1）已知角
终边经过点P（－4，3），求
的值？
（2）已知函数
，(b＞0)在
的最大值为
，最小值为-
，求2a+b的值？
计算：
⑴
；
（2）