已知抛物线
与x轴的一个交点为A(-1，0)，与y轴正半轴交于点C．
直接写出抛物线的对称轴，及抛物线与
轴的另一个交点B的坐标；当∠ACB=90°时，求抛物线的解析式；
抛物线上是否存在点M，使得△ABM和△ABC的面积相等（△ABM与△ABC重合除外）？若存在，请直接写出点M坐标；若不存在，请说明理由．
在第一象限内，抛物线上是否存在点N，使得△BCN的面积最大？若存在，求出这个最大值和点N坐标；若不存在，请说明理由．
点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a－b|．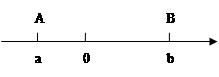
回答下列问题：
（1）数轴上表示2和7两点之间的距离是，数轴上表示3和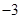
两点之间的距离是．
（2）数轴上表示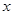
和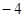
的两点之间的距离表示为．
（3）若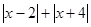
=6，则x的取值范围是．
（4）若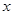表示一个有理数，则代数式
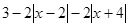有最大值吗？若有，请求出最大值.若没有，说出理由．
已知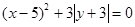
，
， 
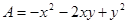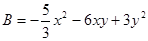， （1）求
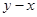的值。
（2）求
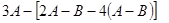的值。
为了能有效地使用电力资源,县城跃进花苑实行居民峰谷用电，居民家庭在峰时段（上午8:00~晚上21:00）用电的电价为0.55元/千瓦时，谷时段（晚上21:00~次日晨8:00）用电的电价为0.35元/千瓦时．若某居民户某月用电100千瓦时，其中峰时段用电x千瓦时．
（1）请用含x的代数式表示该居民户这个月应缴纳电费；
（2）利用上述代数式计算，当x=50时，求应缴纳电费．
阜宁县各中小学校在新学年强势推进“双语阅读”工作。某校图书馆平均每天借书90册，如果某天借书95册，就记作＋5；如果某天借书88册，就记作－2．上星期图书馆借出图书记录如下表：
| 星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| 0 |
＋7 |
＋9 |
－6 |
－5 |
（1）上星期五借出图书是多少册？
（2）上星期二比上星期五多借出图书多少册？
（3）上星期平均每天借出图书多少册？
先化简，再求值：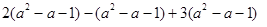
，其中
．