如图,点P1、P2、……Pn是反比例函数y=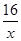 在第一象限图像上,点A1、A2……An在X轴上,若△P1OA1、△P2A1A2……△PnAN-1AN均为等腰直角三角形,则:
在第一象限图像上,点A1、A2……An在X轴上,若△P1OA1、△P2A1A2……△PnAN-1AN均为等腰直角三角形,则: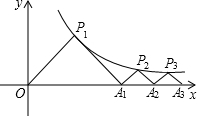
(1)P1点的坐标为
(2)求点A2与点P2的坐标;
(3)直接写出点An与点Pn的坐标.
某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表表示:
| 等级(x级) |
一级 |
二级 |
三级 |
… |
| 生产量(y台/天) |
78 |
76 |
74 |
… |
(1)已知护眼灯每天的生产量y(台)是等级x(级)的一次函数,请直接写出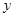 与
与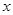 之间的函数关系式:_____;
之间的函数关系式:_____;
(2)每台护眼灯可获利z(元)关于等级x(级)的函数关系式:______;
(3)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?
如图,抛物线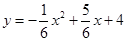 与直线
与直线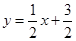 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.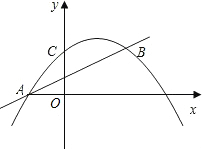
(1)求点A、B的坐标;
(2)若点P是直线x=1上一点,是否存在△PAB是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
如图,抛物线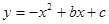 与x轴交与点A(1,0)与点B, 且过点C(0,3),
与x轴交与点A(1,0)与点B, 且过点C(0,3),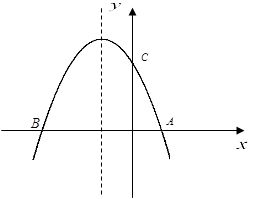
(1)求该抛物线的解析式;
(2)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.
如图,反比例函数 的图象与一次函数
的图象与一次函数 的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.
的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.
(1)求一次函数和反比例函数的解析式;
(2)当y1≥3时,求x的取值范围;
(3)求使y1>y2时x的取值范围.