在△ABC中,顶点A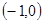 ,B
,B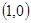 ,动点D,E满足:①
,动点D,E满足:①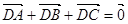 ;②
;②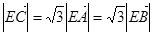 ,③
,③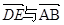 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)是否存在圆心在原点的圆,只要该圆的切线与顶点C的轨迹有两个不同交点M,N,就一定有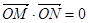 ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由.
从1,2,3,4,5,6中不放回地随机抽取四个数字,记取得的四个数字之和除以4的余数为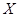 ,除以3的余数为
,除以3的余数为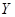
(1)求X=2的概率;
(2)记事件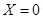 为事件
为事件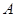 ,事件
,事件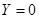 为事件
为事件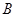 ,判断事件
,判断事件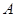 与事件
与事件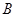 是否相互独立,并给出证明.
是否相互独立,并给出证明.
如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC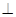 平面ABC.
平面ABC.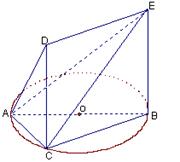
(1)证明:平面ACD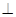 平面
平面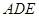 ;
;
(2)若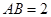 ,
,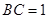 ,
,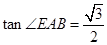 ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.
已知向量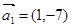 ,
,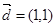 ,对任意
,对任意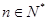 都有
都有 .
.
(1)求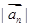 的最小值;
的最小值;
(2)求正整数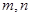 ,使
,使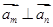
在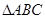 中,角
中,角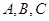 所对的边分别为
所对的边分别为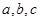 ,函数
,函数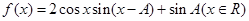 在
在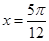 处取得最大值.
处取得最大值.
(1)求角A的大小.
(2)若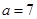 且
且 ,求
,求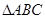 的面积.
的面积.
已知函数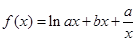 (
(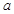 、
、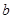 为常数),在
为常数),在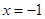 时取得极值.
时取得极值.
(1)求实数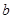 的取值范围;
的取值范围;
(2)当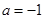 时,关于
时,关于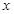 的方程
的方程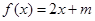 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数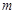 的取值范围;
的取值范围;
(3)数列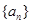 满足
满足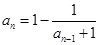 (
(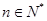 且
且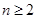 ),
),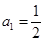 ,数列
,数列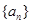 的前
的前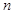 项和为
项和为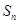 ,
,
求证: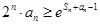 (
(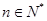 ,
,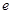 是自然对数的底).
是自然对数的底).