．（本小题满分12分）
某化妆品生产企业为了占有更多的市场份额，已在2011年度进行一系列促销活动，经过市场调查和测算，化妆品的年销量x万件与年促销费t万元之间满足3-x与t+1成反比例,如果不搞促销活动，化妆品的年销量只能是1万件。已知2011年生产化妆品的设备折旧、维修等固定费用为3万元，每生产1万件化妆品需再投入32万元的生产费用。若将每件化妆品的售价定为：其生产成本的1.5倍与“平均每件促销费的一半”之和，则当年生产的化妆品正好能销完。
（1）将2011年的利润y(万元)表示为促销费t（万元）的函数
（2）该企业2011年的促销费投入多少元时，企业的年利润最大？
（注：利润=销售收入-生产成本-促销费，生产成本=固定费用+生产费用）
已知
，函数
．
（1）求
的对称轴方程；
（2）若对任意实数
，不等式
恒成立，求实数
的取值范围．
已知学生的数学成绩与物理成绩具有线性相关关系，某班6名学生的数学和物理成绩如表：
| 学生 学科 |
 |
 |
 |
 |
 |
 |
数学成绩（ ） |
83 |
78 |
73 |
68 |
63 |
73 |
物理成绩（ ） |
75 |
65 |
75 |
65 |
60 |
80 |
（1）求物理成绩对数学成绩的线性回归方程；
（2）当某位学生的数学成绩为70分时，预测他的物理成绩．
参考公式：用最小二乘法求线性回归方程
的系数公式：
参考数据：
，
某学校对高一800名学生周末在家上网时间进行调查，抽取基中50个样本进行统计，发现上网的时间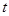
（小时）全部介于0至5之间．现将上网时间按如下方式分成五组：第一组
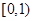，第二组
，第三组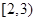
，第四组
，第五组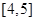
，下图是按上述分组方法得到的频率分布直方图．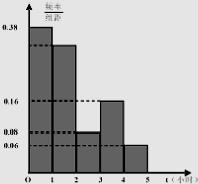
（1）求该样本中上网时间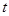在范围内的人数；
（2）请估计本年级800名学生中上网时间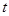在范围内的人数；
（3）若该样本中第三组只有两名女生，现从第三组中抽两名同学进行座谈，求抽到的两名同学恰好是一名男生和一名女生的概率．
已知函数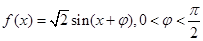
，且
．
（1）求
的解析式；
（2）已知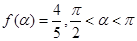
，求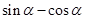
．
已知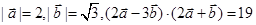
．
（1）求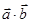
的值；（2）若
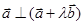，求
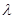的值