(本小题满分13分)
为加强大学生实践、创新能力和团队精神的培养,促进高等教育教学改革,教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序.通过预赛,选拔出甲、乙等五支队伍参加决赛.
(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;
(Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
某同学用“五点法”画函数 在某一个周期的图象时,列表并填入了部分数据,如下表:
在某一个周期的图象时,列表并填入了部分数据,如下表:
(1)请求出上表中的 ,
, ,
, ,并直接写出函数f(x)的解析式;
,并直接写出函数f(x)的解析式;
(2)将f(x)的图象沿x轴向右平移 个单位得到函数g(x),若函数g(x)在
个单位得到函数g(x),若函数g(x)在 (其中
(其中 )上的值域为
)上的值域为 ,且此时其图象的最高点和最低点分别为P,Q,求
,且此时其图象的最高点和最低点分别为P,Q,求 与
与 夹角
夹角 的大小.
的大小.
近两年来,各大电视台都推出了由明星参与的游戏竞技类节目。高一某研究性学习小组在长沙某社区对50人进行第一时间收看该类节目与性别是否有关的收视调查,其中20名女性中有15名第一时间收看该类节目,30名男性中10名第一时间收看该类节目.
(1)根据以上数据建立一个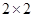 列联表,并判断第一时间收看该类节目是否与性别有关?
列联表,并判断第一时间收看该类节目是否与性别有关?
(2)该研究性学习小组共有A、B、C、D和E五名同学,五人分成两组模拟“撕名牌”的游戏,其中一组三人,一组两人,求A、B两同学分在同一组的概率.
参考数据: .
.
临界值表:
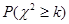 |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
函数 数列
数列 的前
的前 项和
项和 ,且
,且 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式 成立.
成立.
(1)求函数 的表达式;
的表达式;
(2)求数列 的通项公式.
的通项公式.
已知数列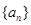 满足
满足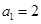 ,
,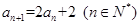 .
.
(1)求证:数列 是等比数列,并求出通项公式
是等比数列,并求出通项公式 ;
;
(2)若数列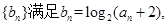 设
设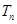 是数列
是数列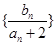 的前
的前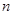 项和,求证:
项和,求证: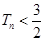 .
.
如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 且
且 ,
, ,
, 分别为
分别为 ,
, 的中点;
的中点;
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.