如图所示，两块平行金属板M、N正对着放置，s1、s2分别为M、N板上的小孔
，s1、s2、O三点共线，它们的连线垂直M、N，且s2O=R..以O为圆心、R为半径的圆形区域内同时存在磁感应强度为B、方向垂直纸面向外的匀强磁场和电场强度为E的匀强电场.D为收集板，板上各点到O点的距离以及板两端点的距离都为2R，板两端点的连线垂直M、N板。质量为m、电荷量为+q的粒子，经s1进入M、N间的电场后，通过s2进入电磁场区域，然后沿直线打到光屏P上的s3点.粒子在s1处的速度和粒子所受的重力均不计.求：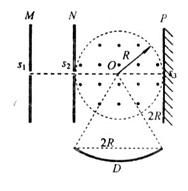
M、N两板间的电压为R；
撤去圆形区域内的电场后，当M、N间的电压改为U1时，粒子恰好垂直打在收集板D的中点上，求电压U1的值及粒子在磁场中的运动时间t；
撤去圆形区域内的电场后，改变M、N间的电压时，粒子从s2运动到D板经历的时间t会不同，求t的最小值。
如图所示,重力为G1=10 N的物体A与重力为G2=50 N的物体B用跨过定滑轮的轻绳连接,B物体放在水平桌面上,且绳的BO段水平 ,AO段竖直,已知B与桌面间的最大静摩擦力Fm=8 N,为使A､B均保持静止,可对B物体加一个水平向左的拉力F,试确定拉力F的大小应满足的条件.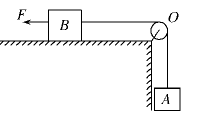
如图,人重600 N,木块A重400 N,人与A､A与地面的动摩擦因数均为0.2,现人用水平力拉绳,使他与木块一起向右做匀速直线运动,滑轮摩擦不计,求:
(1)人对绳的拉力;
(2)人脚对A的摩擦力的方向和大小.
如图所示,劲度系数为k2的轻质弹簧,竖直放在桌面上,上面压一质量为m的物体,另一劲度系数为k1的轻质弹簧竖直地放在物体上面,其下端与物块上表面连接在一起,要想物体在静止时,下面弹簧承受物重的2/3,应将上面弹簧持上端A竖直向上提高多大的距离?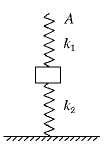
如图所示,为一轻质弹簧的长度L和弹力F的大小关系图线,试由图线确定: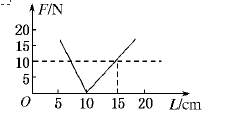
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧伸长0.15 m时,弹力的大小.
如图所示,半径为R､内壁光滑的空心圆筒放在地上,将两个重力都是G､半径都是r的球(R<2r<2R)放在圆筒中,求:
(1)筒底对球A的弹力?
(2)筒壁对球A的弹力是否大于筒壁对球B的弹力?
(3)球A对球B的弹力一定大于重力G吗?
(4)球B对筒壁的压力一定小于重力G吗?