如图所示，有两本完全相同的书A、B，书重均为5 N，若将两本书等分成若干份后交叉地叠放在一起置于光滑桌面上，并将书A固定不动，用水平向右的力F把书B匀速抽出，现测得一组数据如下：
| 实验次数 |
1 |
2 |
3 |
4 |
… |
n |
| 将书分成的份数 |
2 |
4 |
8 |
16 |
… |
逐页交叉 |
| 力F的大小(N) |
4.5 |
10.5 |
22.5 |
46.5 |
… |
190.5 |
根据以上数据，试求：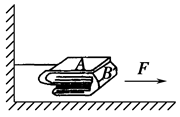
若将书分成32份，力F应为多大？
该书的页数．
该书任意两张纸之间的动摩擦因数为多少？
汽车发动机的额定功率为60kW，汽车的质量为5×103 kg，运动中所受阻力的大小恒为车重的0.1倍。
（1）若汽车以恒定功率启动，汽车所能达到的最大速度是多少?当汽车速度达5m／s时的加速度多大?
（2）若汽车以恒定加速度0.5m／s2启动。则这一过程能维持多长时间?
(19分)如图所示，足够长的光滑绝缘水平台左端固定一被压缩的绝缘轻质弹簧，一个质量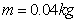
、电量
的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度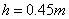
，倾斜轨道与水平方向夹角为
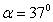、倾斜轨道长为
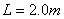，带电小球与倾斜轨道的动摩擦因数
。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强
。（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
（1）被释放前弹簧的弹性势能？
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径应该满足什么条件？
（3）如果竖直圆弧轨道的半径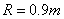
，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？
如图所示，在xoy平面直角坐标系的第一象限有射线OA，OA与x轴正方向夹角为30°，OA与y轴所夹区域内有沿y轴负方向的匀强电场E1，第二象限存在水平向右的匀强电场E2（未知），其它区域存在垂直于坐标平面向外的匀强磁场。有一质量为m、电量为q的带正电粒子，从y轴上的P点沿着x轴正方向以初速度v0射入电场，运动一段时间后经过Q点垂直于射线OA进入磁场，经磁场垂直x轴进入偏转电场E2，过y轴正半轴上的P点再次进入匀强电场E1，已知OP=h，不计粒子重力，求：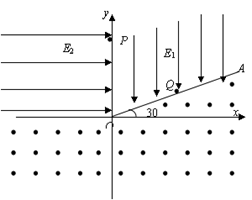
(1)粒子经过Q点时的速度大小；
(2)匀强电场电场强度E1的大小；
(3)粒子从Q点运动到P点所用的时间。
如图所示，质量m=2.2kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动。（cos37°=0.8，sin37°=0.6，取g=10m/s2）
求：
（1）金属块与地板间的动摩擦因数；
（2）如果从某时刻起撤去拉力，撤去拉力后金属块在水平地板上滑行的最大距离。
“嫦娥一号” 的成功发射，为实现中华民族几千年的奔月梦想迈出了重要的一步。已知“嫦娥一号”绕月飞行轨道可以近似看成圆周，距月球表面的高度为H，飞行周期为T,月球的半径为R，万有引力常量为G，假设宇航员在飞船上,飞船在月球表面附近竖直平面内俯冲， 在最低点附近作半径为r的圆周运动，宇航员质量是m，飞船经过最低点时的速度是v；。求：
(1)月球的质量M是多大？
(2)经过最低点时，座位对宇航员的作用力F是多大？