(19分)如图所示，足够长的光滑绝缘水平台左端固定一被压缩的绝缘轻质弹簧，一个质量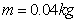
、电量
的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度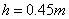
，倾斜轨道与水平方向夹角为
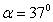、倾斜轨道长为
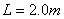，带电小球与倾斜轨道的动摩擦因数
。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强
。（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
（1）被释放前弹簧的弹性势能？
（2）要使小球不离开轨道（水平轨道足够长），竖直圆弧轨道的半径应该满足什么条件？
（3）如果竖直圆弧轨道的半径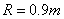
，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？
如图所示，虚线MO与水平线PQ相交于O，二者夹角θ=30°，在MO左上侧存在电场强度为E、方向竖直向下的匀强电场，MO右下侧某个区域存在磁感应强度为B、垂直纸面向外的匀强磁场（图中未画出），磁场的一条边界在直线MO上，现有一质量为m、电量为+q的带电粒子在纸面内以速度v=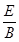
，且方向与MO成
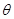角从M点射入磁场，又向左从MO上的D点（图中未画出）射出磁场进入电场，最后到达O点，不计粒子重力。求：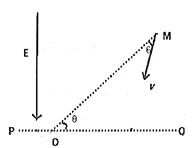
（1）MD的距离L；
（2）粒子从M点运动到O点所用的时间
（3）磁场区域的最小面积。
如图甲所示，一倾角θ=30°的斜面固定在水平地面上，现有一木块以初速度vo=4m/s的速度沿斜面上滑，电脑通过测速仪画出木块从开始上滑至最高点的v-t图线，如图乙所示。（g取l0m/s2）求：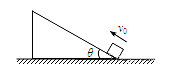
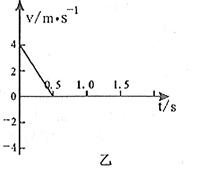
甲
（1）木块与斜面间的动摩擦因数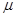
；
（2）木块回到出发点时的速度大小v。
如图所示，传送带与地面成夹角θ=37°，以10m/s的速度逆时针转动，在传送带上端轻轻地放一个质量m=0．5kg的物体，它与传送带间的动摩擦因数μ=0．5，已知传送带从A→B的长度L=16m，则物体从A到B需要的时间为多少？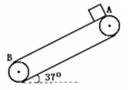 
汽车正以10m/s的速度在平直公路上前进，发现正前方有一辆自行车以4m/s的速度同方向做匀速直线运动，汽车应在距离自行车多远时关闭油门，做加速度为6m/s2的匀减速运动，汽车才不至于撞上自行车?
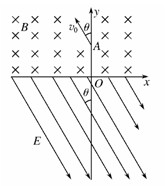
如图所示，在x轴的上方有磁感应强度为B的匀强磁场，方向垂直纸面向里．在x轴的下方有电场强度为E的匀强电场，方向与y轴负方向成θ角．一个带电量为+q、质量为m的粒子以初速度v0从A点进入磁场．v0方向与磁场方向垂直，与y轴正方向成θ角．粒子从x轴射出磁场的速度恰与射入磁场时的速度反向（即与电场方向相同）；不计重力。求：（1）粒子在磁场中运动的时间t;（2）粒子进入电场之后，直至到达y轴的过程中，运动的距离S，（3）粒子进入电场之后，直至到达y轴的过程中，电势能的变化量Δε