古代学者认为,物体下落的快慢是由它们的重量大小决定的,物体越重,下落得越快,古希腊哲学家亚里士多德最早阐述了这种看法;但是这种从表面上的观察得出的结论实际是错误的。伟大的物理学家伽利略用简单明了的科学推理,巧妙地揭示了亚里士多德的理论内容包含的矛盾。他在1638年写的《两种新科学的对话》一书中指出:根据亚里士多德的论断,一块大石头的下落速度要比一块小石头的下落速度大,假定大石头下落速度为8,小石头下落的速度为4,当我们把石头拴在一起时,下落快的会被下落慢的拖着而减慢,下落慢的会被下落快的拖着而加快,结果整体系统的下落速度应该小于8.但是两块石头拴在一起,加起来比大石头还要重,根据亚里士多德的理论,整个系统的下落速度应该大于8.这样就使得亚里士多德的理论陷入了自相矛盾的境地.伽利略由此推断重的物体不会比轻的物体下落得快.根据伽利略的推理方法,假设用两块同样重的石头为研究对象,你又如何推翻亚里士多德的结论呢?(回答应简明)
用重力公式及牛顿第二定律又如何推翻亚里士多德的结论呢?
(9分)一列横波在x轴上传播,在t1 = 0时刻波形如图中实线所示,t2 = 0.05s时刻波形如图中虚线所示.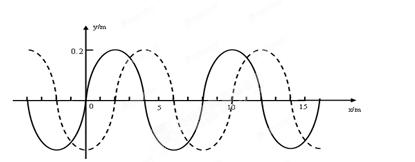
①求这列波的波速是多少
②若有另一列波能与这列波发生稳定干涉,则另一列波的最小频率是多少?
(9分)如图所示,一定质量的气体温度保持不变,最初,U形管两臂中的水银相齐,烧瓶中气体体积为800ml;现用注射器向烧瓶中注入200ml水,稳定后两臂中水银面的高度差为25. 3cm;已知76cm高的水银柱产生的压强约为l.0×105Pa,不计U形管中气体的体积。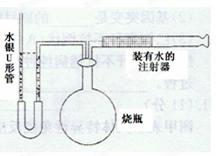
求:①大气压强
②当U形管两边液面的高度差为45.6cm(左高右低)时,烧瓶内气体的体积。
(17分)如图所示,在倾角为θ的粗糙斜面上,一个质量为m的物体被水平力F推着静止于斜面上,物体与斜面间的动摩擦因数为μ,且μ<tanθ,求力F的取值范围.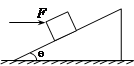
(15分)高速公路上甲、乙两车在同一车道上同向行驶,甲车在前,乙车在后,速度均为v0=30m/s,距离s0=100m,t=0时刻甲车遇紧急情况后,甲、乙两车的加速度随时间变化如图所示,取运动方向为正方向。通过计算说明两车在0~9s内会不会相撞?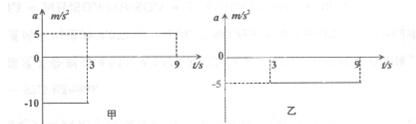
当物体从高空下落时,所受阻力会随物体的速度增大而增大,因此经过下落一段距离后将匀速下落,这个速度称为此物体下落的收尾速度。研究发现,在相同环境条件下,球形物体的收尾速度仅与球的半径和质量有关.下表是某次研究的实验数据
| 小球编号 |
A |
B |
C |
D |
E |
| 小球的半径(×10-3m) |
0.5 |
0.5 |
1.5 |
2 |
2.5 |
| 小球的质量(×10-6kg) |
2 |
5 |
45 |
40 |
100 |
| 小球的收尾速度(m/s) |
16 |
40 |
40 |
20 |
32 |
(1)根据表中的数据,求出B球与C球在达到终极速度时所受阻力之比.
(2)根据表中的数据,归纳出球型物体所受阻力f与球的速度大小及球的半径的关系(写出有关表达式、并求出比例系数).
(3)现将C号和D号小球用轻质细线连接,若它们在下落时所受阻力与单独下落时的规律相同.让它们同时从足够高的同一高度下落,试求出它们的收尾速度;并判断它们落地的顺序.